∠ 1 = ?°, на 55° больше, чем ∠ 2.
∠ 2 = ?°
Оба угла являются смежными.
Решение:Пусть x° равен смежный ∠ 2, тогда ∠ 1 равен (55+x)˚. Зная, что свойство смежных углов всегда содержит сумму 180°, составим уравнение с переменными и решим задачу алгебраическим
Составление математической модели:
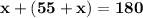
Работа с математической моделью:
Поскольку уравнение имеет переменные, раскроем скобки и найдём значение переменных:
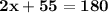
Теперь, зная что число с переменной и число без переменной в данном случае вычислить невозможно, перенесем число без переменной в правую часть уравнения (число становится отрицательным):
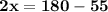
Затем вычислим полученный пример, находящийся в правой части уравнения:
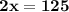
Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель:
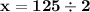
ответ математической модели:
Исходя из значения данного примера, получим корень уравнения:
 ˚ - ∠ 2.
˚ - ∠ 2.
Теперь остаётся только узнать величину ∠ 1:
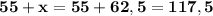 ˚ - ∠ 1.
˚ - ∠ 1.
Відповідь:
13 см, 13 см, 24 см
Пояснення:
Дано: ΔАВС, АВ=ВС, Р=50 см, АК⊥АС, АК=5 см
Знайти: АВ, ВС, АС-?
Рішення:
Р= 2АВ+АС; → 2АВ = 50-АС ;
Так як АК висота рівнобедренного трикутника, то вона є і медіаною для АС, отже АК= АС/2
Розглянемо ΔАКВ, Де ∠К= 90°, АК= АС/2
За теоремою Піфагора АВ²=АК²+ ВК²;
АВ²= АС²/4+25; / * 4( домножимо обидві частини на 4)
4АВ²= АС²+100; ( Підставимо в ліву частину данні з підкресленої формули)
(50- АС)² =АС²+100;
2500-100АС+АС²= АС²+100;
АС²-АС²-100АС=100-2500;
-100АС= -2400; /: (-100)
АС= 24 (см)
2АВ=50-24=26(см)
АВ=ВС=26см/2=13см
,