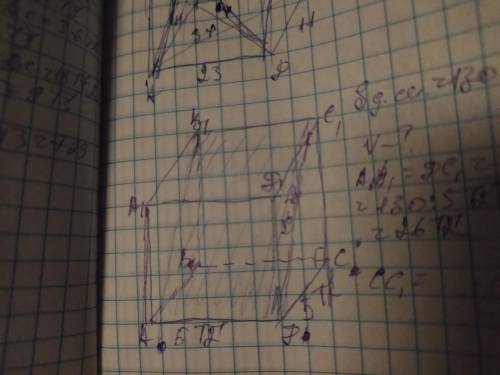
В основе правильной четырёхугольной призме лежит квадрат. Диагональным сечением призмы является прямоугольник, и так как известна его площадь, найдём его вторую сторону по формуле обратной формуле площади:
АВ1=ДС1=130÷5√2=26√2см
Вторая сторона диагонального сечения также является диагональю в гранях АА1В1В и ДД1С1С. Диагональ делит эти грани на 2 равных прямоугольных треугольника, в которых сторона основания и высота призмы являются катетами а диагональ гипотенузой. Зная сторону и диагональ найдём высоту призмы по теореме Пифагора:
ДД1²=С1Д²-СД2=(26√2)²-(5√2)²=
=676×2-25×2=1352-50=1302; ДД1=√1302см
Теперь найдём объем призмы, зная стороны и высоту по формуле:
V=а²×h, где а- стороны основания, а h-высота призмы:
V=(5√2)²×√1302=25×2×√1302=
=50√1302см³
ОТВЕТ: V=50√1302см³
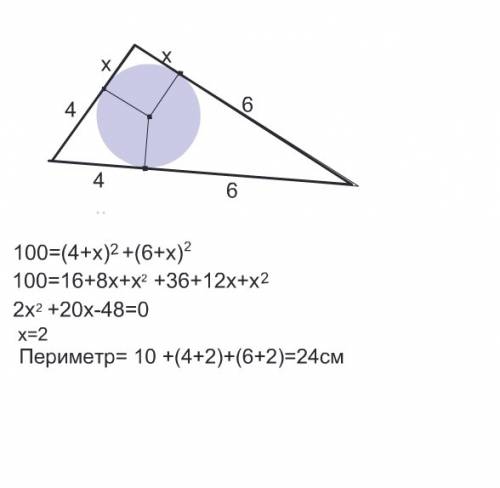
Гипотенуза равна
4+6=10см
По свойству касательных к окружности меньший катет равен меньшему отрезку гипотенузы и неизвестному отрезку касательной у прямого угла
Больший катет равен большему отрезку гипотенузы и неизвестному отрезку касательной у прямоуго угла. Обозначим эти отрезки ( они равны) х.
Составим уравнение нахождения гипотенузы по теореме Пифагора:
100=(4+х)² +(6+х)²
После преобразований получим квадратное уравнение
2х²+20х-48=0
Решив уравнение чере дискриминант D=784,
получим два корня. Один из них (-12) отрицательный и не подходит.
х=2
Имеем 3 стороны треугольника:
катет 4+2=6 см
катет 6+2=8 см
гипотенузу 10 см
Периметр треугольника равен 24 см
AH=5.
HD=9
BH=4
проведем CE высота
AB=CD ⇒ AH=ED
HE=9-5=4 ⇒ BC=4
AD=5+9=14
S=1/2*(4+14)*4=18*0.5*4=36