ответ. 102.
Объяснение:
Решение. Проведем отрезки BD и CE. Пусть они пересекаются в точке О. Заметим, что треугольники BCD и CDE равнобедренные с углом 108 при вершине, а значит, углы при основании равны 36 (они отмечены на рисунке одной дугой). Тогда BCE = BDE = 72. Угол COD равен 108 (т.к. в треугольнике COD два угла по 36). Поэтому COB = 180108 = 72. Углы по 72 отмечены на рисунке двумя дугами. Получаем, что треугольники CBO и DEO равнобедренные. Значит, AB = BO =BC = CD = DE = EO = х. Заметим, что OBA = 9636 = 60. Значит, треугольник OBA равнобедренный с углом 60 при вершине, т.е. равносторонний. Поэтому AO = x. Вычислим угол AOE AOE = EOBAOB = 10860 = 48. Треугольник AOE равнобедренный с углом 48 при вершине. Поэтому OEA = (18048)/2 = 66. Получаем, что угол E пятиугольника равен AED = AEO+OED = 66+36 = 10
Найдем второй отрезок гипотенузы для каждого случая.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.⇒
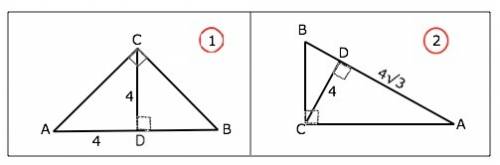
a)
СD²=АD•ВD
16=4•BD
BD=16:4=4⇒
Высота СD - медиана и биссектриса ∆ АВС и делит его на два равнобедренных прямоугольных треугольника.
Острые углы такого треугольника равны 45°
б)
СD²=АD•ВD
16=4√3•BD⇒
BD=16:4√3=4/√3
Из ∆ САD:
tg∠САD=CD:AD=4:4√3=1/√3- это тангенс 30°
Из ∆ CВD:
tg∠СBD=BD:CD=(4/√3):4=√3 - это тангенс 60°
Острые углы этого треугольника 30° и 60°
Большая высота треугольника проведена к меньшей стороне.
Воспользуемся двумя формулами для нахождения площади треугольника:
формулой Герона: S = √(p·(p - a)(p - b)(p - c))
и S = 1/2 ah, где а - меньшая сторона треугольника, h - искомая высота.
a = 9 см, b = 10 см, с = 17 см.
p = (9 + 10 + 17)/2 = 18 см
S = √(18 · 9 · 8 · 1) = 9 · 4 = 36 cм²
S = 1/2 ah
h = 2S / a
h = 2 · 36 / 9 = 8 см