смотри ниже
Объяснение:
2. уравнение прямой: y=kx+C; Эта прямая пересекает ось 0Y в точке C, а тангенс угла между этой прямой и осью 0X равен k.
Если прямая параллельна оси 0X, то угол между прямой и этой осью равен нулю. Тангенс нуля тоже равен нулю, значит k=0. Получаем уравнение прямой, параллельной оси 0X: y=0*x+C; то есть y=C
Значит в задании 2. уравнение прямой имеет вид y=-2
3. подставляем значение абсциссы (x=1) в уравнение и находим нужные точки.
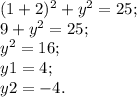
Первая точка (1;4) вторая (1;-4)
4. уравнение окружности
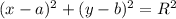
Где (a;b) координаты центра окружности.
В данном уравнении 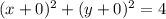
центр окружности находится в начале координат (0;0), значит наша прямая совпадает с осью 0Y и описывается уравнением x=0
5. прямая y=8 параллельна оси абсцисс 0X, значит диаметр окружности равен 8, а радиус равен 4.
Площадь прямоугольного треугольника равна 84 дм², а радиус окружности, вписанной в этот треугольник, 3см. Найти катеты треугольника.
Пусть дан треугольник АВС, угол С=90º
Точки касания вписанной окружности на АС- точка К, на ВС - точка Н, на гипотенузе АВ- точка М.
Пусть АК=х, ВН=у.
Тогда по свойству отрезков касательных из одной точки АМ=х, ВМ=у
АВ=х+у
АС=х+3, ВС=у+3
Формула радиуса вписанной окружности
r=S:p, где r -радиус, S - площадь треугольника. р- его полупериметр
р=х+у+3
3=84:(х+у+3)
х+у+3=28⇒
х+у=25
у=25-х
АВ=х+у=25 дм
АС=х+3
ВС=25-х+3=28-х
По т.Пифагора
(х+3)²+(28-х)²=625
Произведя вычисления и приведя подобные члены, получим квадратное уравнение
х²-25х+84=0
D=25²-4·84=289
Решив уравнение, найдем два корня: 21 и 4
АС=21+3=24 дм
ВС=28-21=7 дм
Кстати, длины сторон этого треугольника из Пифагоровых троек, где стороны относятся как 7:24:25

Медиана тр-ка делит тр-к на два равновеликих. То есть Sabm = Smbc = 1/2(Sabc)
Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон. То есть ВР/РС = 1/3. В таком же отношении делится биссектрисой и площадь тр-ка, т.е Sabp/Sapc = 1/3. То есть Sabp = 1/4(Sabc), а Sapc = 3/4(Sabc). В тр-ке АВМ та же биссектриса делит площадь тр-ка АВМ в отношении 1:1,5 (так как АМ = 1/2 АС, потому что ВМ - медиана). Отсюда Sakm = 3/4*Sabm = 1/2:4*3 = 3/8(Sabc)
Smkpc = Sapc-Sakm = 3/4 - 3/8 = 3/8.
Тогда Sakm/Smkpc = (3/8):(3/8) = 1/1.