угол ВСД + угол СДА = 180 градусоа, так основания трапеции параллельны , а углы односторонние . Биссектрисы разделили каждый из этих улов пополм , значит угол GCD + угол CDG = 180⁰ :2 =90⁰ .Угол СGD = 90⁰ . Значит Δ GCD - прямоугольный . Найдём CD по теореме Пифагора
CD =√ 24² +18² =√ 900 =30
ответ CD = 30
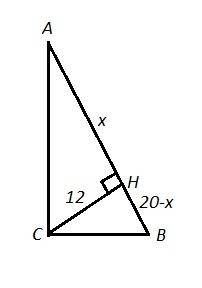
Если высота СН прямоуг. ΔАВС равна 12 см ,то гипотенуза АВ не может равняться 20 см.
По свойству высоты, проведённой из прямого угла прямоуг. треуг-ка на гипотенузу, она есть среднее пропорциональное (среднее геометрическое) между проекциями катетов на гипотенузу, то есть CH²=AH·BH .
Если гипотенуза АВ=20 см, то АВ=АН+ВН=20 см .
Обозначим АH=х , тогда ВН=(20-х) см.

Уравнение не имеет действительных корней, значит не существует треугольника с гипотенузой 20 см и высотой, проведённой из вершины прямого угла , равной 12 см.
1) ABCD - трапеция => ^C+^D=180. (^-угол)
2) Т.к. CG и DG - биссектрисы=>^GDC=1/2*^D; ^GCD=1/2*^C;
3) ИЗ 1 и 2=>^GCD+^GDC=90*=>^DGC=180-90=90=>GCD- прямоугольный треугольник=>DG^2+CG^2=CD^2=324+576=900.
CD=30