AD пересекает BC = K;
AK = KD;
BK = KC;
Доказать:AB || CD.
Доказательство:AK = KD (по условию); |
BK = KC (по условию); |=> △AKB = △CKD (по I признаку).
∠АКВ = ∠CKD, они вертикальные |
Из этого следует, что накрест лежащие ∠KAB = ∠KDC => AB || CD.
Что и требовалось доказать!Задание #2 (рисунок в файле):Дано:△ABC - равнобедренный;
BD - биссектриса;
∠CKO = 110˚;
DM = DK;
O ∈ BD;
M ∈ AD;
K ∈ CD.
Найти:∠MOD = ?˚.
Решение:∠CKO + ∠OKD = 180˚, т.к. они смежные => ∠OKD = 180˚ - 110˚ = 70˚.
Биссектриса, проведённая к основанию равнобедренного треугольника, является и медианой и высотой.
=> ∠BDC = ∠BDA = 90˚ => △ODK и △ODM - прямоугольные.
Сумма острых углов в прямоугольном треугольнике равна 90°.
=> ∠DOK = 180˚ - (90˚ + 70˚) = 180˚ - 160˚ = 20˚.
MD = DK (по условию); OD - общий катет => △ODM = △ODK.
=> ∠DOK = ∠MOD = 20˚.
ответ: ∠MOD = 20˚.
Объяснение: ЗАДАНИЕ 1
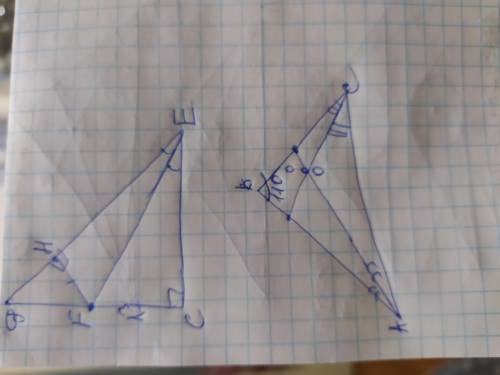
Расстояние от точки до прямой - это длина перпендикуляра, обозначим его FH, поэтому FH перпендикулярно ДЕ. Рассмотрим ∆EFH и ∆EFC. Они прямоугольные, поскольку FH- перпендикуляр, а угол С=90°, поэтому угол С=углу FAE=90°. Так как биссектриса EF делит угол Е пополам, то угол НЕF=углу FEC. Так как один из острый углов одного прямоугольного треугольника равен другому, то вторые острые углы их тоже будут равны. Поэтому угол EFH=углуEFC, и ∆EFH=∆EFC по второму признаку: по двум углам и стороне между ними. Следовательно FC=FH=13см
ответ: FH=13см
ЗАДАНИЕ 2.
Если брать в расчёт, что это угол АВС=110°(т.е. угол В), то сумма углов А и В=180-110=70°; угол А+ угол В=70°, так как сумма углов треугольника составляет 180°
Рассмотрим ∆АОС. Угол АОС=180-(угол ОАС+угол АСО). Поскольку биссектрисы разделяют эти углы пополам их можно записать так:
угол АОС=180–(уголА/2+угол В/2)=
180-(угол А+ угол В)/2. Мы нашли сумму этих двух углов и подставим теперь из значение:
Угол АОС=180–70/2=180-35=145°
ОТВЕТ: угол АОС=145°
ЗАДАНИЕ 3 - практическое. ответ внизу на фото
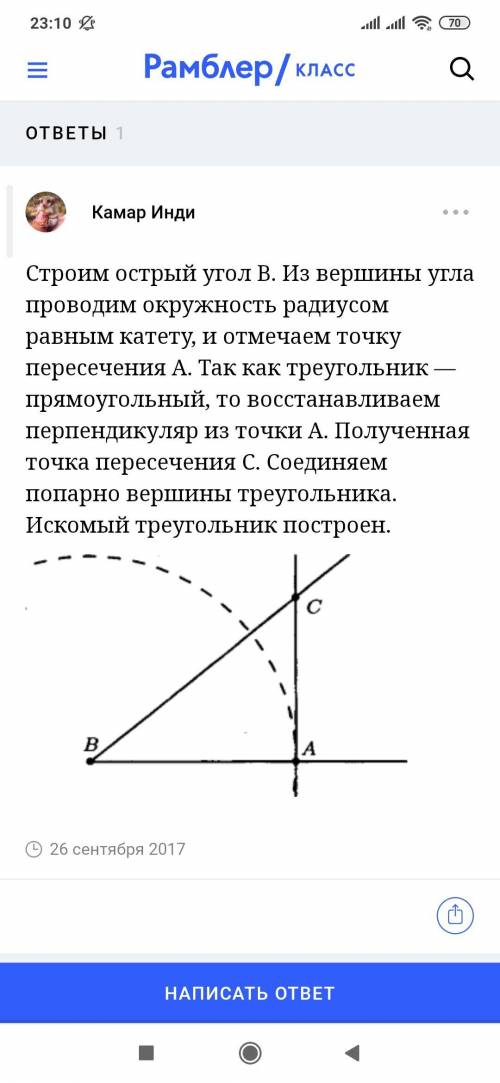
Это должен быть не равносторонний, а равнобедренный. У равнобедренного треугольника есть две стороны (12 см • 2) и основание (5 см). И стороны ВСЕГДА больше основания. Поэтому: 12 • 2 + 5 = 29 см
P = 29 см