Объяснение:
Периметр треугольника - сумма длин всех сторон.
Данный треугольник равнобедренный.
Основание 10 см, боковые стороны по 15 см.
Р=10+15*2=40 см.
Площадь треугольника - S=ah/2, где a - сторона треугольника, h - васота проведенная к ней.
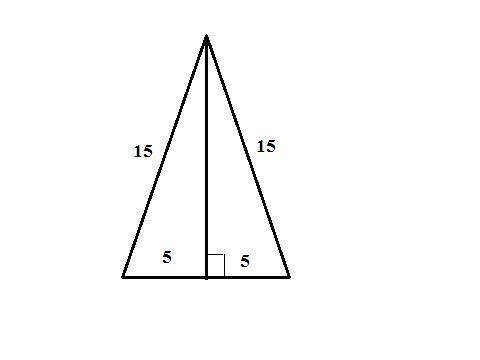
Из вершины равнобедренного треугольника проведем высоту к основанию. По свойству высоты проведенной из вершины она является так-же и медианой. Следовательно высота, половина основания и боковая сторона образуют прямоугольный треугольник, где катет (высота) находится по т. Пифагора - √(15²-5²)=10√2 см.
Тогда площадь треугольника - 10*10√2/2=50√2 см².
СУММА векторов. Начало второго вектора совмещается с концом первого, сумма же есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом второго.
РАЗНОСТЬ. Для получения вектора разности (c) = (a-b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b) (вычитаемое), а концом — конец вектора (a) (уменьшаемое).
Исходя из этого:
1) |AB+BC|=|AC|, то есть |AB+BC|= а.
2) |AB+AC|=|AB+BC1|=|AC1|. АС1 - диагональ параллелограмма, построенного на векторах АВ и АС и вектор АС1 равен 2*АО. Вектор АО- высота равностороннего треугольника и равен а*√3/2. Значит АС1=а*√3.
|AB+AC|=а*√3.
3) |AB+CB|=|AB+C1B1|=|A1B1|. Вектор СВ переносим в конец вектора АВ, получаем вектор С1В1. Сумма - вектор АВ1. Вектор АВ1 по модулю равен вектору АС1.
|AB+CB|=а*√3.
4) |ВА-ВC|=|CA|=а.
5) |АВ-АC|=|CВ|=а.