Объяснение:
Рассмотрим линейную функцию y = 3 ∙ x, определенную на числовом отрезке [−2; 3]. Эта функция является прямой пропорциональностью с угловым коэффициентом k = 3, графиком которой является прямая линия, проходящая через начало координат. Так как k < 0, то функция y = − 3 ∙ x является убывающей, то есть большему значению аргумента соответствует меньшее значение функции:
х = 3 – наибольшее значение аргумента на числовом отрезке [−2; 3];
y = 3 ∙ 3 = 9 − наименьшее значение линейной функции y = 3 ∙ x на отрезке [−3; 3].
ответ: 9 − наименьшее значение линейной функции y = 3 ∙ x на отрезке [−3
Уравнение окружности имеет вид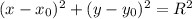 
, где 
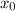и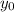 
- координаты центра окружности, а 
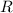- её радиус.
Координаты центра заданной окружности (2; 6).
1. То, что окружность касается оси Ох, значит, что её радиус равен расстоянию от центра окружности до оси абсцисс. На оси Ох ордината равна нулю, а значит, радиус окружности равен 6. Таким образом, уравнение окружности в этом случае: 
.
2. То, что окружность касается оси Оy, значит, что её радиус равен расстоянию от центра окружности до оси ординат. На оси Oy абсцисса равна нулю, а значит, радиус окружности равен 2. Таким образом, уравнение окружности в этом случае: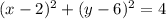 
.
Если sin в какой то точке равен 1/2, то cos в этой точке равен √3/2.
Тангенс в этой точке равен отношению синуса к коинусу в этой точке, он равен 1 / √3.
Тоже самое можно проделать через формулы тригонометрии.
sin t = 1/2
cos t = √( 1 - sin² t) = √3 / 2
tg t = sin t / cos t = 1 / √3
Удачи.