При решении я предполагаю, что автору задачи известно, что медианы делят треугольник на шесть, равных по площади, как отностятся площади треугольников, если есть общая высота и прочее... если что будет не понятно - спршивайте.
1. Skldc = (1/3)*Sabc = 8;
2. (3/4)*Sabc = m*n/2 (прямая MN - средняя линяя, и отсекает четверть площади треугольника); Sabc = 2*m*n/3;
3. Треугольники СОА и СОМ равны - это прямоугогльные треугольники с равными углами и общим катетом. АО = ОМ, поэтому треугольники АОL и LOM тоже равны.
Но самое главное, BL/AL = СВ/АС = 2*CM/AC = 2*MO/OA = 2.
Поэтому Smlb = 2*Smla = 4*Solm, а Smlb + Smla = Sabc/2;
Имеем
4*Solm + 2*Solm = Sabc/2; Solm = 1/12;
4. Это то же самое, что найти площадь треугольника со сторонами 27,29 и 26*2 = 52; понять это очень просто - треугольник достраивается до параллелограмма (медиану продолжаем за основание на свою длину и соединяем полученную точку с концами сторон). Диагонали делят праллелограмм на 2 части, равные по площади. Поэтому и получается, что площадь треугольника со сторонами a,b и медианой m равна площади треугольника со сторонами a, b и 2*m. Считаем по формуле Герона (слава Гейтсу, есть Excel) полупериметр p= 54, p-a = 27;p-b = 25; p - c1 = 2; (c1 это 52 = 2*26); ясно видно, что произведение равно 27^2*100, то есть площадь 270.
5. Всё, что надо знать - формула S = a*b*sinC/2; Доли площадей треугольников АЕМ EBF и MFC от площади АВС определяются именно по ней, к примеру
Saem = (1/3)*AB*(2/5)*AC*sinC/2 = (1/3)*(2/5)*Sabc;
Sefm/Sabc = 1 - (1/3)*(2/5) - (2/3)*(1/6) - (5/6)*(3/5) = 23/90;
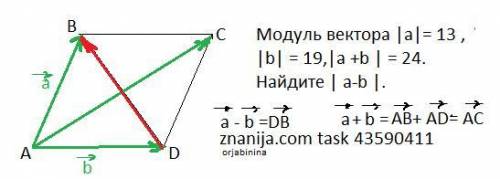
Модуль вектора |a|= 13 ,|b| = 19,|a +b | = 24. Найдите | a-b |.
Объяснение:
1) Рассмотрим ΔАВС, вектор а лежит на стороне АВ, вектор b лежит на стороне АD . Разность векторов а-b=DВ ( вектор) Уточняю длина ( или модуль) вектора равна длине отрезка на котором он лежит. Значит нужно найти отрезок DВ и АВ=13,АD=19 .
2) Достроим ΔАВD до параллелограмма , тогда сумма векторов а+b=АВ+АD=( по правилу параллелограмма ) = вектору АС. Тогда |AC|=|a+b|=24. Значит длина отрезка АС=24. По свойству диагоналей параллелограмма АО=12( О-точка пересечения диагоналей).
3) По свойству диагоналей параллелограмма: "сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон " имеем: AC²+BD²=2(AB²+AD²)
24²+BD²=2(13²+19²), BD=√(2*(169+361)-576)=√484=22.
Треугольник назыввется равнобедренным, если две его стороны равны.
1 Свойство:
В равнобедренном треугольнике углы при основании равны.
рассмотрим равнобедренный треугольник АВС с основанием ВС и докажем, что угол В = углу С. Пусть АD - биссектрисса треуглльника АВС. Треугольники ABD и ACD равны по первому признаку равенства треугольников (АВ = АС - по условию, АD - общая сторона, угол ABD = углу DAC, так как AD - биссектрисса). В равных треугольниках против равных сторон лежат равные углы, поэтому угол В = углу С.
2 Свойство:
В равнобедренном треугоьнике биссектриса, проведенная к основанию, является медианой и высотой.
Рассмотрим треугольник АВС - равнобедренный с основанием ВС, АD - его биссектрисса.
Из равенства треугольников ABD и ACD следует, что BD = DC и угол BDA = углу ADC. Равенство BD = DC означает, что точка D - середина стороны ВС и поэтому AD - медиана треугольника АВС.
Так как угол BDA = углу ADC - смежные, следовательно эти углы прямые, следовательно AD - высота.