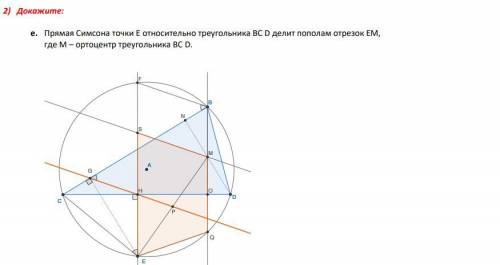
Дано:
Окружность (O;R)
ΔAOB
AB = 32 дм
OC = 12 дм
-----------------------------------
Найти:
C - ?
1. Хорда AB = 32 дм
OC = 12 дм (расстояние от центра до хорды)
AC = CB = 1/2AB = 1/2 × 32 дм = 16 дм
2. ΔOCB — прямоугольный, так как ∠BCO — прямой.
По теореме Пифагора: BO = √OC² + CB²
BO = √(12 дм)² + (16 дм)² = √144 дм² + 256 дм² = √400 дм² = 20 дм ⇒ R = BO = 20 дм
3. Воспользуемся формулой длины окружности, именно по такой формуле мы найдем длину окружности: C = 2πR
C = 2π × 20 дм = 40π дм = 40×3,14 дм = 125,6 дм
ответ: C = 125,6 дм
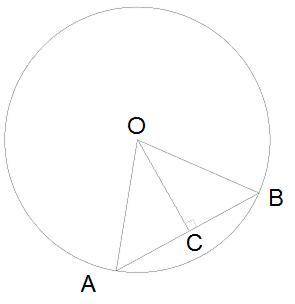
DOA = 70°. Дано в задаче.
BOC = DOA = 70°. Вертикальные углы равны (1).
DOC = 180° - 70° - 110°. Смежные углы в сумме дают 180° (2).
AOB = DOC = 110°. (1).
ODC = (180° - 110°) / 2 = 35°. Сумма углов треугольника равна 180° (3). Если треугольник равнобедренный, то углы при его основаниях равны (4).
ADO = 90° - 35° = 55°. Два угла составляют прямой угол (5).
OAD = ADO = 55°. (4).
OAB = 90° - 55° = 35°. (5).
OBA = OAB = 35°. (4).
OBC = 90° - 35° = 55°. (5).
OCB = OBC = 55°. (4).
Все остальные углы состоят из других и их можно посчитать по сумме. Например:
DAB = DAO + BAO = 55° + 35° = 90°.