
номер 2
Объяснение:
За середнім пропорційним у прямокутному трикутнику.
квадрат катета = добутку гіпотези на проекцію гіпотези
квадрат висоти = добутку проекцій гіпотенузи

Движение - это преобразование фигуры, которое сохраняет расстояние между ее точками.
Свойства движения:
1. Три точки, лежащие (нележащие) на одной прямой, при движении переходят в три точки, лежащие (нележащие) на одной прямой.
2. При движении прямая переходит в прямую - луч - в луч.
3. Отрезок движением переводится в отрезок.
4. Движение соханяет меры углов.
5. Последовательное выполнение двух движений есть движение.
Доказательство свойства 3. Как известно, отрезок - это часть прямой, ограниченная двумя точками. Т.к. по свойству 2 прямая переходит в прямую, то прямая, содержащая отрезок, переходит в прямую, содержащую, отрезок. А так движение сохраняет расстояние, от отрезок одной прямой переходит в равный ему отрезок другой прямой.
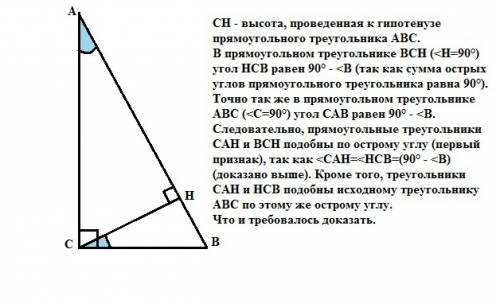
СН - высота, проведенная к гипотенузе прямоугольного треугольника АВС. В прямоугольном треугольнике ВСН (<H=90°) угол НСВ равен 90° - <B (так как сумма острых углов прямоугольного треугольника равна 90°). Точно так же в прямоугольном треугольнике АВС (<С=90°) угол САВ равен 90° - <B. Следовательно, прямоугольные треугольники САН и ВСН подобны по острому углу (первый признак), так как <CAH=<HCB=(90° - <B) (доказано выше). Кроме того, треугольники САН и НСВ подобны исходному треугольнику АВС по этому же острому углу.
Что и требовалось доказать.
Объяснение:
№2)
СН=√(ВН*НС)=√(5*20)=√100=10
ВС=√(ВН*ВА)=√(5*25)=√125=5√5
СА=√(НА*ВА)=√(20*25)=√500=10√5
ответ: СН=10; ВС=5√5; СА=10√5
№3)
Теорема Пифагора
KN=√(MN²-MK²)=√(25²-10²)=√(625-100)=√525=5√21
ME=MK²/MN=100/25=4
EN=25-4=21
KE=√(ME*EN)=√(4*21)=√84=2√21
ответ: KN=5√21; ME=4; EN=21; KE=2√21