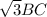Question

В ΔABC ∠C - тупой, а точка D выбрана на продолжении AB через точку B так, что ∠ACD = 135°. Точка D' симметрична D относительно BC. Точка D'' симметрична D' относительно АС и лежит на BC. Известно, что CD'' = $\sqrt{3}BC$ ; AC = 6. Доказать, что ΔCBD - равнобедренный.

Answer 1

Δ СMD = Δ CMD' по построению симметричной точки D' ⇒
СD=CD'
Δ СPD' = Δ CPD'' по построению симметричной точки D''⇒
СD'=CD''

СD = CD' = CD''

BС – серединный перпендикуляр к DD' ⇒
BD=BD'

Обозначим
∠ СD'D= ∠ CDD'= α
∠ CD'D'' = ∠ CD''D'= β

Проведем DK ⊥ AC;
DK || D'D''
Δ CDK – прямоугольный равнобедренный треугольник.
∠CDK =∠ KСD=45o

PD'DK – прямоугольная трапеция.
Cумма углов, прилежащих к стороне DD' равна 180o
∠CDK +∠ СDD'+ ∠ DD'C+ ∠ CD'D'' =180o ⇒
45o+ α + α + β =180o ⇒
2 α + β =135o

В прямоугольном треугольнике MD'D''
сумма острых углов равна 90 o

∠ DD'C+ ∠ CD'D'' + ∠ CD''D' =90o ⇒
α + β+β =90o

Решаем систему двух уравнений:
{2 α + β =135o
{α + 2β =90o

Умножаем первое уравнение на 2:
{4α + 2β =270o
{α + 2β =90o

Вычитаем из первого второе
3α=180o
α =60o

Δ СDD' – равносторонний.
BD=BD' ⇒ B – равноудалена от двух вершин равностороннего треугольника, значит равноудалена и от третьей.
BD=BD'=ВС
BD=BC и значит Δ СBD – равнобедренный, что и требовалось доказать.