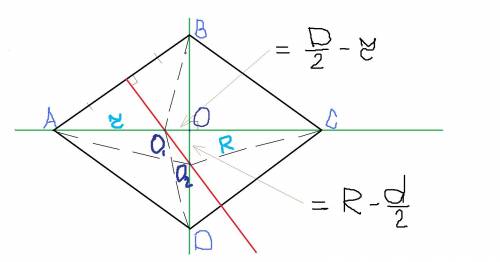
АВСD - ромб
О1 - центр меньшей окружности с радиусом r
O2 - центр большей окр. с рад. R
D - большая диагональ (АС)
d - меньшая диаг. (BD)
а - сторона ромба
Возьмем АВ, поделим пополам и проведем перпендикуляр (на рис. красный)
Точка пересечения его с большой диаг. будет центром меньшей окр., а с меньшей диаг - центром большей окр.
Из треуг. ОСО2 получаем
R^2=(D/2)^2+(R-d/2)^2
Из треуг. ОВО1:
r^2=(d/2)^2+(D/2-r)^2
Решаем эту систему, учитывая, что
a^2=(D/2)^2+(d/2)^2=Dr=dR
получаем
a=2Rr/sqrt(R^2+r^2)
При R=4 , r=3 получим а=4.8
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности. Периметр шестиугольника равен 48 => сторона равна 48/6=8; то есть радиус описанной окружности равен 8. Если вписать в эту окружность квадрат то его диагональ - это диаметр окружности - то есть 16, стороны квадрата пусть будут х, тогда по теореме пифагора (диагональ и две стороны квадрата образуют прямоугольный треугольник - гипотенуза это диагональ квадрата а кататы равны между собой - стороны квадрата)
х²+x²=16²
2х²=256
х²=128
х=8√2