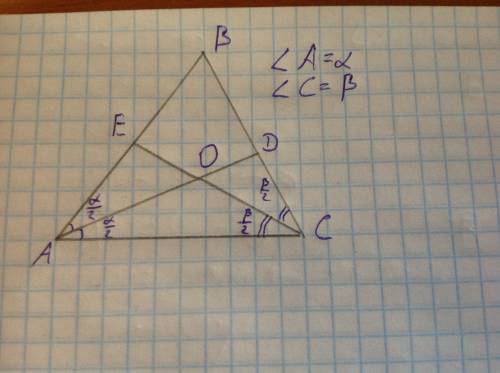
Задание 1.
Пусть х -основание треугольника, тогда боковые стороны (х-2).
Составим уравнение х=(х-2)+(х-2)=32
отсюда х=12, а боковая сторона 12-2=10см.
ответ: боковые стороны треугольника равны 10см.
Задание 2.
Рассмотрим треугольник HCB (он прямоугольный, т.к. CH-высота и угол HCВ равен 30градусам по условию), значит угол В равен 180-90-30=60градусов.
Также мы знаем, что катет лежащий против угла в 30 градусов равен половине гипотенузы, значит поскольку катет ВН равен 3, то гипотенуза СВ равна 3*2=6.
Теперь рассмотрим треугольник ACB (он прямоугольный Угол С равен 90градусов, т.к по условию AC параллельно СВ и угол В равен 60 градусов), значит угол А равен 180-90-60=30градусов.
В треугольнике ACH угол ACH равен 180-90-30=60градусов.
Треугольники ACH и HCB равны. Значит AC=CB равно 6.
По теореме Пифагора 6^2+6^2=72.
Значит АВ равна корень из 72
356м
Объяснение:
Дано:
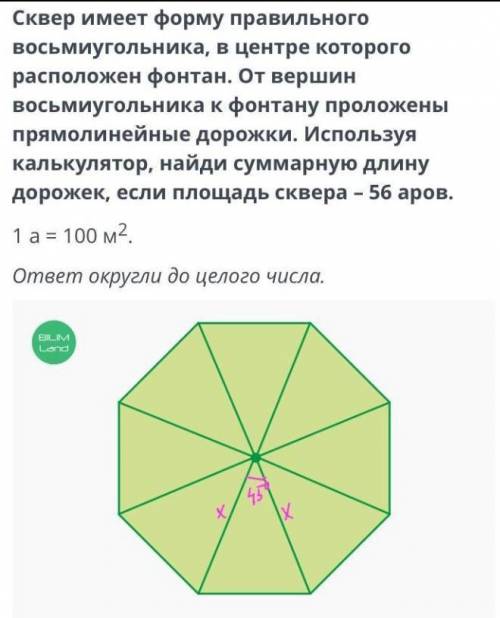
Восьмиугольник.
Sв.=56ар
1ар=100м.
8R=?
Решение.
1)56*100=5600 м площадь восьмиугольника.
2)5600:8=700м площадь одного треугольника образованного радиусами
Из формулы нахождения площади равнобедренного треугольника.
S=1/2*x²*sin<(xx), где х -это сторона треугольника, и она является радиусом восьмиугольника.
Найдем радиус.
700=1/2*R²*sin45°
sin45°=√2/2
700=1/2*R²*√2/2
R²=700*4/√2
R²=1400√2
R=√1979,89899.
R=44,4960559.
8R=8*44,4960559=355,968447м.
Округлить до целого числа.
355,968447≈356 м сумма длин всех радиусов восьмиугольника.