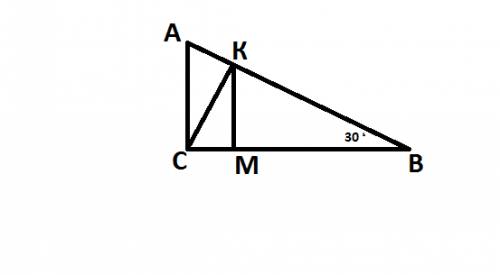
1)тр.СКВ-прямоуг. угол В= 30 градусов то СК=1/2*СВ=9 см
2)тр.КМВ-прямоуг. то угол МКВ=90-30=60 градусов
тр.СКВ-прямоуг. , угол СКМ=90-60=30
3)тр.СМК-прямоуг., угол СКМ=30, то СМ=1/2*СК; СМ=4,5
МВ=18-4,5=13,5
Вы, возможно, ошиблись в условии, и нужно найти площадь треугольника АВС, а не АВD?
Иначе для чего дана длина стороны ВС и отрезка DС? Сделаем рисунок к задаче.
Рассмотрим ⊿ ВDС.
Катет ВD=12 см, гипотенуза ВС=13 см.
С отрезком DС основания они составляют "египетский" треугольник, поэтому этот отрезок равен 5 см.
Треугольник АВD - также прямоугольный, а так как угол А=45°, он и равнобедренный.
Отрезок АD основания равен высоте ВD=12 см
Основание АС треугольника АВС равно
АС=АD+DС=12+5=17 см
S ᐃ АВС=ВD·АС⠰2=102 см²
Вы, возможно, ошиблись в условии, и нужно найти площадь треугольника АВС, а не АВD?
Иначе для чего дана длина стороны ВС и отрезка DС? Сделаем рисунок к задаче.
Рассмотрим ⊿ ВDС.
Катет ВD=12 см, гипотенуза ВС=13 см.
С отрезком DС основания они составляют "египетский" треугольник, поэтому этот отрезок равен 5 см.
Треугольник АВD - также прямоугольный, а так как угол А=45°, он и равнобедренный.
Отрезок АD основания равен высоте ВD=12 см
Основание АС треугольника АВС равно
АС=АD+DС=12+5=17 см
S ᐃ АВС=ВD·АС⠰2=102 см²
В тр-ке СКМ угол СМК = 90°, угол СКМ = углу АВС = 30°, как острые углы с взаимно перпендикулярными сторонами.
В тр-ке АСК, угол АКС = 90°, угол АСК = 30°
В тр-ке АВС найдём АС.
АС = ВС·tg 30° = 18/√3 = 6√3
В тр-ке АКС найдём КС.
КС = АС·cos 30° = 6√3 · 0,5√3 = 9
В тр-ке СКМ найдём СМ.
СМ = КС· sin 30° = 9·0,5 = 4,5
MВ = ВС - СМ = 18 - 4,5 = 13,5(см)