Ну конечно в ЕГЭ нужно все подробно расписывать там по 1,2 признаку подобия и тд. Думаю, сам как нужно распишешь....
Проведем KO∥AA1
И сделаем проекцию KM на пл ABC
Это будет прямая OM
Рассмотрим плоскость основания, в нем проведем высоту BH-она делит основание AC пополам, так как по условию треугольник равнобедренный
Но тут не трудно заметить, что △AMO подобен △AHB с коэффициентом подобия равным 2. Значит MO∥BH и MO перпендикулярно AC
Теперь т о 3-х перпендикулярах. Если прямая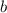 
перпендикулярна проекции прямой на плоскость. То такая прямая 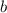перпендикулярна этой прямой.
У нас MO перпендикулярна AC значит по т о 3-х перпендикулярах KM перпендикулярна прямой AC ч.т.д
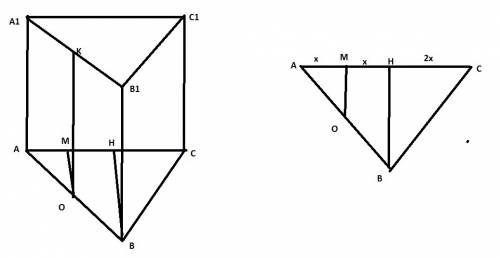
Ромб ABCD, окружность проходит через точки A, B, C
AK = 5 см; КС = 1, 4 см ⇒ АС = АК + КС = 5 + 1,4 = 6,4 см
У ромба диагонали перпендикулярны и точкой пересечения делятся пополам : AC⊥BD; AO=OC = AC/2 = 6,4 /2 = 3,2 см; BO=OD.
AK⊥BD и делит хорду BD пополам ⇒ AK - диаметр окружности.
ΔABK - прямоугольный, так как сторона AK является диаметром описанной окружности.
Высота треугольника, проведенная из прямого угла на гипотенузу, есть среднее геометрическое проекций катетов на гипотенузу :
BO² = AO·OK = AO·(AK-AO) = 3,2·(5-3,2) = 3,2·1,8 = 5,76 = 2,4²
BO = 2,4 см
ΔAOB образован диагоналями, прямоугольный. Теорема Пифагора
AB² = AO² + BO² = 3,2²+2,4² = 10,24+5,76= 16 = 4²
AB = 4 см
ответ: сторона ромба равна 4 см
Радиус основания конуса равен 6, а высота конуса равна 8.
В конусе проведено сечение плоскостью , проходящей через вершину конуса . Площадь сечения равна 25√3.
Найдите угол между плоскостью основания и плоскостью сечения.
Сделаем рисунок.
Так как сечение АВС ограниченго двумя образующими, оно является равнобедренным треугольником с высотой и медианой ВМ.
АВ=10, это и без вычисления можно сказать - треугольник "египетский" с отношением сторон 3:4:5
Катеты 6 и 8, отсюда гипотенуза АВ=10
Можно сторону АВ найти по т. Пифагора, результат будет тем же.
Рассмотрим треугольник АВМ.
Он прямоугольный с прямым углом ВМА, и
его площадь равна половине площади сечения АВС.
S АВМ=(25√3):2
Из М проведем к образующей ВА высоту МК.
МК=2·S Δ АВМ:АВ
МК=(25√3):10=2,5√3
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
МК²=ВК·АК
Пусть ВК=х, тогда АК=10-х
Составим уравнение:
(2,5√3)²=х·(10-х)
18,75=10х-х²
х²-10х+18,75=0
Найдем корни этого уравнения
D=b²-4ac= -10²-4·1·18,75=25
Так как дискриминант больше нуля, уравнение имеет два корня
х₁=7,5
х₂=2,5
Так как ВК больший отрезок, его длина равна 7,5
Длина второго отрезка не пригодится. (Можно с его найти АМ, затем НМ и косинус искомого угла, но вряд ли стоит, это дольше будет)
ВМ - гипотенуза треугольника ВМН, угол ВМН которого нам нужно найти.
ВМ²=МК²+ВК²
ВМ²=2,5√3²+7,5²
ВМ²=18,75+ 56,25=75
ВМ=5√3
sin ∠ВМН=8:5√3
sin ∠ВМН = 0,9238
По таблице определяем, что
67°< ∠ВМН <68°, т.е приблизительно 67°29' ( точнее можно найти в более подробных таблицах)