Рисунок во вложении.
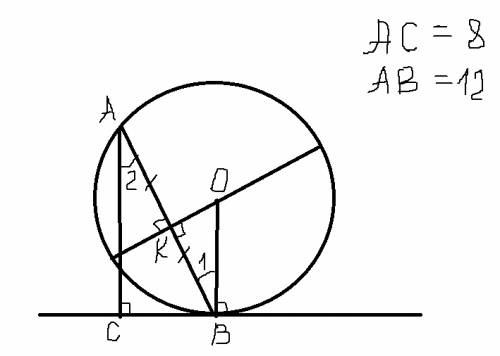
Назовем хорду АВ. Через точку В проведем касательную, из точки А проведем перепндикуляр АС к касательной-это и будет расстоянием от А до касательной. Получили прямоугольный треугольник АВС.
Теперь проведем диаметр окружности перпедикулярно хорде АВ. Он будет делить эту хорду пополам. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам. Точку пересечения хорды и диаметра назовем К .
Проведем радиус ОВ. Так как ОВ перпендикулярен касательной и АС перпендикулярен касательной, то ОВ//АС. Углы 1 и 2 накрест лежащие, значит они равны.
Рассмотрим треугольники АВС и ВОК: они прямоугольные и имеют по равному острому углу, значит они подобны. Из подобия следует, что ОВ:АВ=АС:ВК => ОВ:12=6:8 => ОВ=9
ответ: 9см.
1. У правильных многоугольников все стороны и углы равны. Пермиетр правильного треугольника по стороне а: 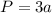
Правильного четырехугольника: 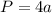
2. Вся окружность соответствует центральному углу в 360 градусов. Очевидно, если мы возьмем половину окружности, то угол так же поделится надвое, а длина дуги будет составлять половину длины окружности. Так же будут относиться и площади.
Длина окружности: 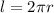 . Тогда, из простейших геометрических соображений, длина дуги l1 будет равна:
. Тогда, из простейших геометрических соображений, длина дуги l1 будет равна: 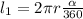 , где α - центральный угол.
, где α - центральный угол.
a) 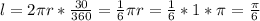
б) 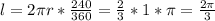
Socн = 0,5 * 11 * 3 = 33/2
V = 1/3*Sосн*h
h=3V/Sосн=3*33/33*2=6
т.к. ребра взаимно перпендикулярны, неизвестное ребро - высота
6.