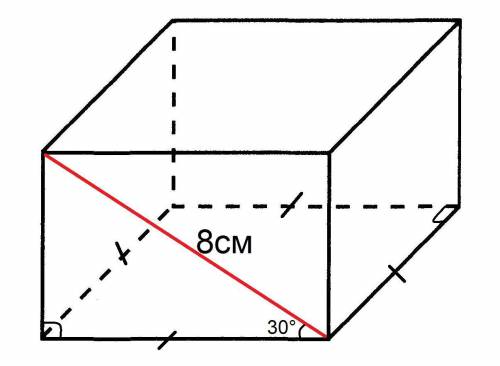
Рассмотрим один из двух треугольников, полученных при проведении диагонали в боковой грани параллелепипеда:
Треугольник прямоугольный т.к. параллелепипед прямой, по этой же причине один из острых углов равен 30°; гипотенуза (диагональ боковой грани) равна 8см; катет лежащий напротив угла в 30° (боковое ребро) равен половине гипотенузы: 8см:2 = 4см; другой катет (сторона основания), по теореме Пифагора, равен √(8²-4²) = √(64-16) = √48 см.
Объём параллелепипеда можно найти через его высоту (в нашем случаи это и боковое ребро) и площадь основания. В основании лежит квадрат, поэтому его площадь равна (√48 см)² = 48 см².
Тогда объём равен 4см · 48см² = 192 см³
ответ: 192см³.
Объяснение:
60) S =(PK+MN)· h/2= 10·10=100 так как средняя линия равна половине сумм оснований, а это 2 радиуса по 5 единиц и высота там равна диаметру -10 ед.
59) ОК =MN/2=20/2=10 так как это радиус окружности
58) ML= MN+LK-NK=2+7-6=3 cложим все части сторон получим : 2+7+6+3=18 (частей) следовательно периметр делим на 18 . 54:18=3 (ед) - составляет 1 часть . Далее MN= 2·3=6 NK=6·3=18 LK=7·3=21 ML=3·3=9
57) АD = 15-8=7 так как сумма противоположных сторон равна 6+9=15 следовательно по свойству вписанной окружности и других противоположных сторон =15! P= BC+CD+AD+AB=8+9+7+6=30 ед