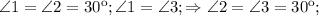 )
) 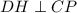 ,
, 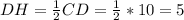 как катет лежащий против угла 30 в треугольнике CHD.
как катет лежащий против угла 30 в треугольнике CHD. 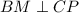 ,
, 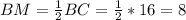 как катет лежащий против угла 30 в треугольнике BMC.
как катет лежащий против угла 30 в треугольнике BMC. 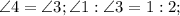
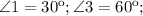 Тогда в ромбе
Тогда в ромбе 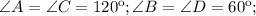
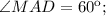 , тогда
, тогда 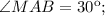 Треугольник BAM равнобедренный, АВ=АМ, тогда
Треугольник BAM равнобедренный, АВ=АМ, тогда 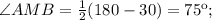
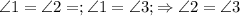 , треугольник MCD равнобедренный, MD=CD=3,
, треугольник MCD равнобедренный, MD=CD=3, 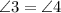 ,
, 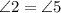 , как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.
, как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.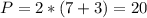 .
.
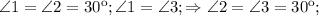 )
) 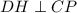 ,
, 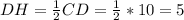 как катет лежащий против угла 30 в треугольнике CHD.
как катет лежащий против угла 30 в треугольнике CHD. 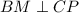 ,
, 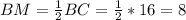 как катет лежащий против угла 30 в треугольнике BMC.
как катет лежащий против угла 30 в треугольнике BMC. 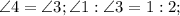
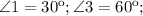 Тогда в ромбе
Тогда в ромбе 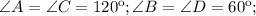
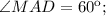 , тогда
, тогда 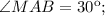 Треугольник BAM равнобедренный, АВ=АМ, тогда
Треугольник BAM равнобедренный, АВ=АМ, тогда 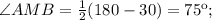
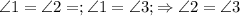 , треугольник MCD равнобедренный, MD=CD=3,
, треугольник MCD равнобедренный, MD=CD=3, 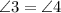 ,
, 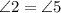 , как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.
, как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.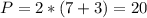 .
.
Высота конуса перпендикулярна основанию и равна радиусу сферы. Тогда по теореме Пифагора получаем