1. Основания равнобедренной трапеции равны. - нет
2. Диагональ любого прямоугольника делит его на 2 равных треугольника. - да
3. Две прямые, параллельные третьей прямой, перпендикулярны друг другу. - нет
4. Вертикальные углы равны. - да
5. Если один из двух смежных углов острый, то другой тупой. - да
6. Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны. - нет
7. Диагонали ромба равны. - нет
8. Существует треугольник с углами 47° , 56° и 87° - нет
9. Любой четырехугольник, у которого все углы равны является квадратом. - нет
10. Медиана любого треугольника делит угол пополам - нет
11. Все углы ромба равны. - нет
12. Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны. - нет
13. Площадь квадрата равна произведению двух его смежных сторон. - да
14. Любой четырехугольник, у которого все стороны равны, является ромбом. - да
15. Сумма углов равнобедренного треугольника равна 180 градусам. - да
16. Существует такой четырехугольник, у которого два противолежащих угла равны, а другие два противолежащих угла не равны. - нет
17. Диагонали параллелограмма равны. - нет
18. У любой трапеции боковые стороны равны. - нет
19. В тупоугольном треугольнике все углы тупые. - нет
20. В любом параллелограмме диагонали точкой пересечения делятся пополам. - да
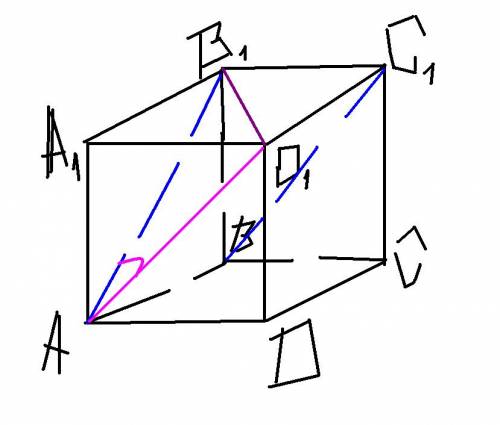
а) BC1 || AD1, поэтому угол между прямыми AB1 и BC1 равен углу между AB1 и AD1.
ребро куба равно а, поэтому (так как грани куба - квадраты), то AB1=AD1=B1D1, а значит треугольник AB1D1 - правильный(равносторонний),
углы равностороннего треугольника равны 60 градусов,
значит искомый угол между прямыми AB1 и BC1 равен 60 градусов
б) так как В1С1 - перпендикуляр с точки С1 на грань АА1В1В, то угол между прямой AC1 и гранью AA1B1B равен углу В1АС1
(треугольник АВ1С1 - прямоугольным с прямым углом АВ1С1)
по свойству диагонали квадрата 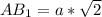
по свойству диагонали куба 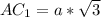
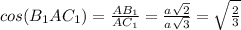
угол В1АС1 равен arccos корень(2/3)т.е.
угол между прямой AC1 и гранью AA1B1B равен arccos корень(2/3) градусов
искомое сечение - симметричный четырехугольник BPKL
диагонали PL , BK пересекаются под углом 90 град
по условию
стороны основания AB=BC=CD=AD =4
боковые ребра MA=MB=MC=MD =8
точка К - середина ребра MD ; KD = MD /2 = 8/2=4
ABCD -квадрат
диагональ AC = BD = 4√2
пересечение диагоналей точка F : BF =FD = BD/2 =4√2 /2 =2√2
BK - медиана треугольника MBD
длина медианы BK = 1/2 √(2 BM^2 +2 BD^2 - MD^2 ) =1/2 √(2*8^2 +2*(4√2)^2 - 8^2 ) =4√2
по теореме косинусов
cos KBD = ( KD^2 - (BK^2+BD^2) )/ (-2*BK*BD)= ( 4^2 - ((4√2)^2+(4√2)^2) )/ (-2*4√2*4√2)= 3/4
MF - высота
треугольник EBF - прямоугольный
BE = BF / cos KBD = 2√2 / 3/4 = 8√2/3
KE = BK - BE =4√2 -8√2/3 =4√2/3
по теореме Пифагора EF =√(BE^2 - BF^2) =√( (8√2/3)^2 - (2√2)^2) =2√14/2
MF - высота
треугольник MFB - прямоугольный
по теореме Пифагора MF =√( MB^2 -BF^2) =√( 8^2- (2√2)^2 ) =2√14
ME =MF -EF =2√14 -2√14/2 = 2√14/2
треугольники MPL ~ MCA подобные
PL / AC = ME /MF ; PL = AC * ME /MF = 4√2 * 2√14/2 /2√14 =2√2
площадь сечения(четырехугольника BPKL)
Sс = PL*BK *sin<BEP /2 = 2√2*4√2*sin90 /2 = 8
ответ 8