Нет возможности построить рисунок. Постараюсь объяснить без него.
Угол между образующей и проекцией на плоскость основания конуса- угол между образующей и плоскостью основания- это угол между образующей и радиусом основания, угол этот равен 30° .Значит, высота конуса лежит против угла в 30° в прямоуг. треугольнике и равна половине гипотенузы, равной 6см и равна эта высота 3см.
Квадрат радиуса тогда равен 6²-4²=20
объем конуса равне произведению трети высоты , т.е. 3*(1/3)=1 на площадь основания, т.е. на 20π
Объем равен 1*20π=20π/см³/
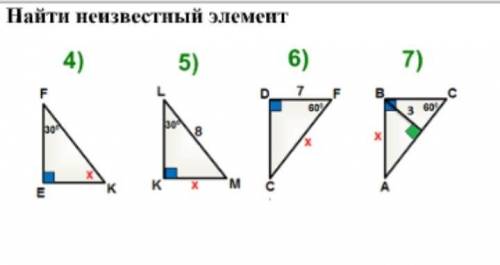
4) Дано: <F
Найти: <K
<F = 30° => <K = 90-<F => <K = 60°.
<K = 60°.
5) Дано: LM, <L
Найти: KM(катет)
<L = 30°
По теорему о 30-градусном угле прямоугольно треугольника: катет, противоположный углу 30 градусов, равна половине гипотенузы. =>
KM = LM/2 = 4
KM = 4.
6) Дано: DF, <F
Найти: CF(гипотенузу)
<F = 60° => <C = 90-<F = 30°
Сторона, противоположная углу <F, это DF
По той же теореме, но обратным путём: CF(гипотенуза) = DF /2 => CF = 7*2 = 14
CF = 14.
7)
Дано: BO, <C
Найти: BA(гипотенузу)
<C = 60° =. <A = 90-<C = 30°
Биссектриса, разделила треугольник на 2 прямоугольного треугольника, так как углы, созданные биссектрисой — равны 90°.
BO = 3 => BA = 3*2 = 6 (так как BO — это стоорна противоположная углу 30 градусов(<A))
BA(гипотенуза) = 6.