пусть начальный сплав весит а кг и в нем х кг серебра
В этот сплав добавили 3 кг серебра, значит в новом сплаве его стало х+3 кг, а вес нового сплава стал а+3 кг
новый сплав стал содержать 90 процентов от веса нового сплава
про серебро составлю тогда уравнение
x+3=0.9(a+3)
x=0.9a-0.3 -первое уравнение будущей системы 2 уравнений с 2 неизвестными
третий сплав получается из начального с добавлением 2 кг сплава, содержащего 90 % серебра, это к х прибавляется 2*0.9=1.8 кг серебра
тогда это можно записать как х+1.8 кг серебра в третьем славе
"получают сплав с 84% массовой долей серебра"-третий сплав стал весом а+2 кг, а серебра в нем 0.84(a+2)
приравняю оба эти выражения
x+1.8=0.84(a+2)-второе уравнение системы
x=0.84a+1.68-1.8=0.84a-0.12
приравнивая оба выражения х
0.9a-0.3=-0.84a-0.12
0.06a=0.18
a=3
тогда серебра в нем 0.9*3-0.3=2.7-0.3=2.4 кг
2.4/3*100=80% серебра в начальном сплаве или 2.4 кг
1)
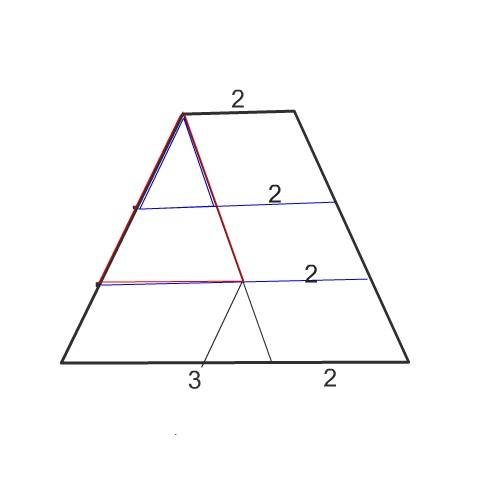
Рассмотрим рисунок этой поделенной на 3 части трапеции.
Поведя из вершины у меньшего основания прямую, параллельную одной из боковых сторон, получили треугольник и параллелограмм.
Каждая из этих фигур разделена на 3 части.
В параллелограмме стороны равны, а части искомых отрезков равны меньшему основанию трапеции.
Треугольник же делится на подобные треугольники по свойству равенства углов при параллелльных прямых ( которые мы провели при разделении трапеции) и секущей, а угол при вершине этих треугольников - общий.
Так как боковая сторона разделена на 3 равные части, то отношение сторон этих треугольников 1:2:3
Основание большего треугольника (его боковая сторона=боковая сторона трапеции) равно разности оснований:
5 - 2=3
Т.к. боковая сторона трапеции разделена на 3 равные части, отношение сторон меньшего ( верхнего) треугольника и большего равно 1:3
Следовательно, его основание равно
⅓ ·3=1 см
Отношение второго по величине треугольника и большего равно
2:3, отсюда его основание равно
⅖·3=2 см
Так как длина каждого из проведенных параллелльных отрезков больше оснований треугольников на 2, то:
длина искомых отрезков равна:
1 см+2=3 см
2см+2=4см
--------------------------------
2)
Стороны треугольника MNP относятся к сторонам АВС как 1:3,т.к. каждая сторона Δ АВС разделена в отношении 1:2. И эта одна часть - сторона Δ MNP, стороне же АВС остаются её 3 части.
Треугольники АВС и MNP подобны, так как их сходственные стороны пропорциональны и коэффициент подобия этих треугольников
k=1/3
Площади подобных фигур относятся, как квадрат их коэффициента подобия, а в этой задаче в отношении (1/3)²=1/9.
Площадь Δ MNP=1/9 площади тр-ка АВС и равна 1/9 от S или S/9
----------------
3)
Площади подобных фигур относятся, как квадрат их коэффициента подобия. Т.к. площади квадратов относятся как 25:9, то коэффициент подобия ( отношение сторон квадратов) равен
k=√(25/9)=5/3
Пусть сторона меньшего квадрата равна х.
Тогда сторона большего равна х+10
(х+10):х=5:3
По свойству пропорции
3(х+10)=5х
3х+30=5х
2х=30
х=15
Сторона меньшего квадрата равна 15
Проверка:
Площадь большего квадрата
(15+10)²=625
площадь меньшего
15²=225
625:225=25:9
Профессорская задачка :)
1. Вс задача. В произвольном треугольнике две прямые, выходящие из разных вершин, делятся в точке пересечения в отношении 2:1 и 1:1. Нужно найти, в каком отношении они делят стороны. На самом деле, для заданной задачи достаточно найти, в каком отношении делится сторона, к которой проведена та прямая, которая длится в отношении 2:1. На первом рисунке - простое решение этой задачи. (Не надо путать обозначения тут и при решении основной задачи).
Задано ВК/KN = 1; AK/KM = 2; надо найти BM/BC.
Проводится PM II AC, треугольники PKM и AKN подобны, и PK/KN = KM/AK = 1/2; но КN = BN/2, то есть PN = BN/4; тогда и BP = BN/4; а отсюда BM = BC/4;
2. Собственно решение. Я изменил обозначение точки пересечения медиан трегольника АВС на букву G. O - центр описанной окружности, Н - ортоцентр. Точка Р пересечения биссектрисы угла А и GН делит GН пополам.
Поскольку АР - биссектриса угла А, то её точка пересечения с окружностью N делит дугу ВС пополам, то есть совпадает с точкой пересечения перпендикуляра к ВС из центра О.
Легко увидеть, что угол DNA между биссектрисой и этим диаметром, обозначенный как α, равен (угол АСВ - угол АВС)/2 (проще всего это понять, если провести через А хорду АА1 II ВС, тогда дуга ВА1 = дуга АС, и угол А1NA = угол А1СА, а DN биссектриса угла A1NA), то есть α = 15°;
Теперь самое главное. Точки O, G и Н лежат на прямой Эйлера, и OG = GH/2; Отсюда следует, что OG = GP = PH; кроме того, точка G делит АК в отношении AG/GK = 2 (ну, это же медиана тр-ка АВС...)
Согласно вс задаче из треугольника AON получается OK = ON/4; то есть расстояние от О до хорды ВС равно четверти радиуса окружности. Отсюда легко найти радиус R описанной окружности. R^2 = 1^2 + (R/4)^2; R = 4/√15;
Для того, чтобы найти площадь, нужно найти АМ. Центральный угол DOA равен 2α = 30°; и равен углу ОАМ, откуда сразу видно, что АМ = ОК + АО*cos(2α) = R*(1/4 + cos(2α)) = R(1/4 + √3/2);
S = ВС*АМ/2 = (4/√15)*(1 + 2√3)/8 = (1 + 2√3)/(2√15);
Я, конечно, мог и ошибиться в арифметике, так что проверяйте, но смысл решения понятен :)