1) Если вокруг квадрата описать окружность, то радиус этой окружности будет равен 1/2 диагонали квадрата. по теореме Пифагора найдем диагональ квадрата :
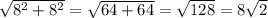 см
см
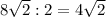 см будет радиус окружности
см будет радиус окружности
Формула длины окружности:
С=2пR.
Подставим наши значения
С= 2*3,14*4√ 2 = 25,12√2 см
ответ: Длина окружности описанной вокруг квадрата равна 25,12√2 см
2) Поскольку окружность вписана в квадрат , то диаметр этой окружности будет равен стороне квадрата, т.е. 8 см. Тогда радиус окружности будет 8/2=4 см
Формула длины окружности: С=2пR.
С= 2*3,14*4= 25.12 см
ответ длинна окружности вписанной в квадрат 25,12 см
угол ВАЕ = угол КСВ (это вписанные углы, опирающиеся на дугу КЕ)
Поэтому треугольники АВЕ и КСВ подобны (угол АВС у них общий, поэтому все углы этих тр-ков попарно равны).
Это означает, что
угол ВКС = угол ВЕА
Поскольку в 4-угольнике ВКМЕ сумма углов 360 градусов (М - точка пересечения СК и АЕ), угол АВС 20 градусов, угол КМЕ 90 градусов, а остальные два угла равны между собой, то
угол ВКС = (360 - угол АВС - 90)/2 = 125 градусов;
Отсюда
угол КСВ = 180 - угол АВС - угол ВКС = 180 - 20 - 125 = 35 градусов.
Раз кроме угла и величины сторон ничего не известно, пытаемся вывернуться за счет теоремы синусов: в треугольнике отношение сторон равно отношению синусов противолежащих им углов. В треугольнике МРК МР/РК = SinX°/Sin45°. Отсюда SinРКМ = SinХ = 6*Sin45°/10 = 0,4243. Угол РКМ ≈ 25°. Значит угол РКО = 45°+25°=70°( так как угол РМК = 45°, а угол МКО = углу РМК как накрест лежащие при параллельных прямых МР и ОК) . По формуле площади параллелограмма S=a*b*Sinα, где a,b - стороны, а α - угол между ними. S = 10*6*Sin70° = 60*0,9397 = 56,4м².