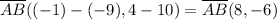 ;
; от точки A
от точки A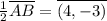 ;
; в обе возможные стороны
в обе возможные стороны перпендикулярен вектору основания
перпендикулярен вектору основания  , а значит его проекции накрест-пропорциональны с противоположным знаком:
, а значит его проекции накрест-пропорциональны с противоположным знаком: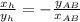 , что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:
, что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:  (II) ;
(II) ; пропорционален вектору
пропорционален вектору  , поскольку для вектора
, поскольку для вектора  выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора
выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора  ;
; имеет длину
имеет длину 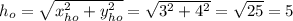 ;
;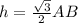 , т.к
, т.к 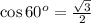 ;
;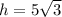 , а стало быть
, а стало быть  ;
;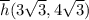 .
.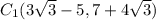 /// примечание:
/// примечание: 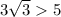 ;
;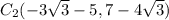 /// примечание:
/// примечание: 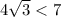 .
.
1)Периметр ромба равен 4*сторона
сторона= 52\4=13 см
Площадь ромба равна произведению квадрата стороны на синус угла между сторонами
отсюда синус угла =площадь робма разделить на квадрат стороны
sin A=120\(13^2)=120\169
Так как угол А -острый,то cos A=корень(1-sin^2 A)=корень(1-(120\169)^2)=
=119\169
По одной из основных формул тригонометрии
tg A=sin A\cos A=120\169\(119\169)=120\119
ответ:120\169,119\169,120\119.
2)
Катеты треугольника относятся друг к другу как 9 к 40.
Пусть длина одного катета 9х, тогда второго 40х.
По теореме пифагора квадрат катетов равен квадрату гипотенузы
(9х) в квадрате + (40х) в квадрате = 82 в квадрате
81 х^2 + 1600 х^2 = 6724. Отсюда х^2 = 4.
х=2.
один катет 9х=18 см
второй катет 40х=80 см
3)
Боковые стороны: (36-10)/2=13
Высота h=корень(169-25)=12
tga=5/12 sina=5/13 cosa=12/13.
4) cos - отношение прилежащего( в данном случае неизвестного) катета к гипотенузе, пусть гипотенуза - х, тогда катет 24х / 25. по теореме пифагора квадрат гипотенузы равен сумме квадратов катетов x^2=14^2+(24x / 25)^2, отсюда х=50, а второй катет равен 48