Рассмотрим прямоугольный треугольник MNP. NH - высота, проведённая к гипотенузе, следовательно, она является средним геометрическим для отрезков MH и HP.
Следовательно :
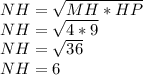
Тогда площадь прямоугольного треугольника MNP равна половине произведения высоты и стороны, к которой проведена эта высота.
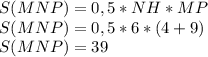
MP - диагональ. Диагональ параллелограмма делит параллелограмм на два равных (в частности и на равновеликих) треугольника. Следовательно, площадь прямоугольника MNPK равна произведению площади треугольника MNP на два.
S(MNPK) = 39*2 = 78.
ответ: 78 (ед^2).
Рассмотрим прямоугольный треугольник MNP. NH - высота, проведённая к гипотенузе, следовательно, она является средним геометрическим для отрезков MH и HP.
Следовательно :
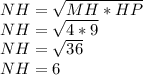
Тогда площадь прямоугольного треугольника MNP равна половине произведения высоты и стороны, к которой проведена эта высота.
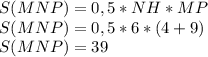
MP - диагональ. Диагональ параллелограмма делит параллелограмм на два равных (в частности и на равновеликих) треугольника. Следовательно, площадь прямоугольника MNPK равна произведению площади треугольника MNP на два.
S(MNPK) = 39*2 = 78.
ответ: 78 (ед^2).
поскольку грани равнонаклонены, то Sboc*cos(Ф) = Sоsn; то есть площадь боковой поверхности равна половине площади боковой поверхности, и, следовательно, 1/3 от полной. Итак, площадь основания 108/3 = 36; сторона 6. Рассмотрим треугольник - сечение пирамиды через апофемы противоположных граней. Поскольку все апофемы равны, это равнобедренный треугольник, а поскольку угол в основании 60 градусов, это правильный треугольник со стороной 6. Высота пирамиды - это высота этого сечения. То есть она равна 6*корень(3)/2 = 3*корень(3).
Объем пирамиды
V = 36*3*корень(3)/3 = 36*корень(3)