Объяснение:
Дано:
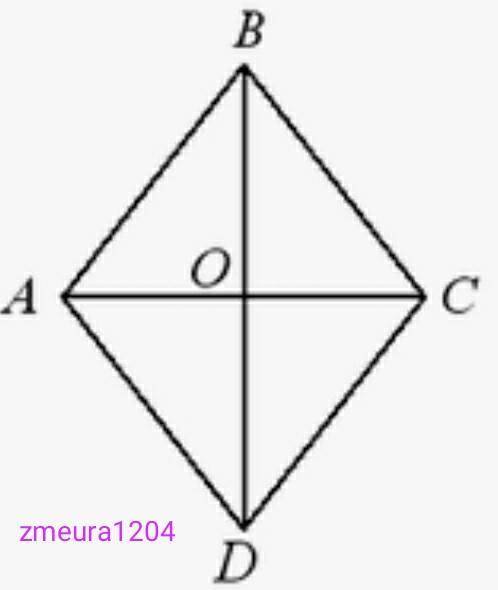
ABCD- ромб
АВ=20см
ВD=32см
АС=?
Решение
Диагонали ромба пересекаются перпендикулярно и точкой пересечения делятся пополам.
ВО=ВD:2=32:2=16см.
∆АОВ- прямоугольный треугольник.
По теореме Пифагора
АО=√(АВ²-ВО²)=√(20²-16²)=√(400-256)=
=√144=12см.
АС=2*АО=2*12=24см.
ответ: АС=24см.
2)
Дано:
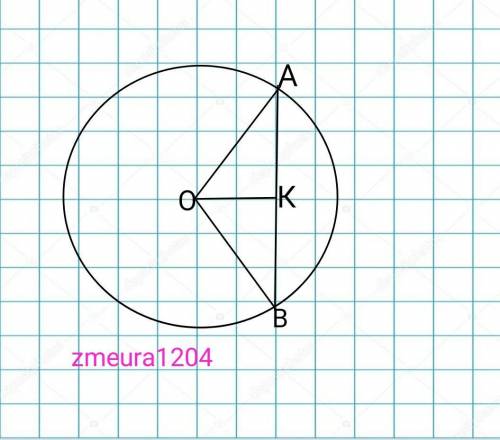
Окружность
О-центр окружности
АВ=8см хорда
ОА=ОВ=R=5см
ОК=?
Решение
ОК- высота, медиана и биссектрисса равнобедренного треугольника ∆АОВ.
ВК=КА
ВК=АВ:2=8:2=4см.
Теорема Пифагора
ОК=√(ОВ²-КВ²)=√(5²-4²)=√(25-16)=3см
ответ: 3см
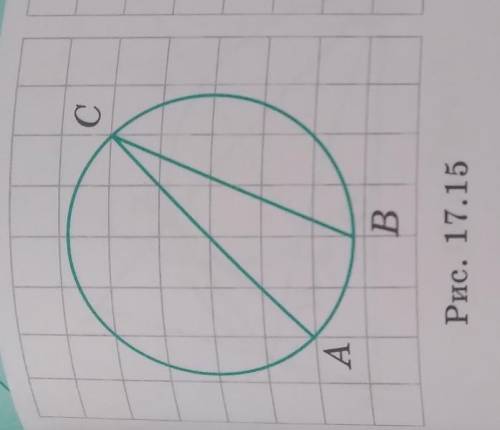
АС - диаметр ⇒ ∠АВС=90° (как угол, опирающийся на диаметр) .
ΔАКС: ∠АКС=90° , АК=КС ⇒ ΔАКС - равнобедренный ⇒
∠АСК=∠САК=45°
ОВ || СК , АС - секущая ⇒ ∠АСК=∠АОВ=45° (соответственные углы)
ОА=ОВ как радиусы ⇒ ΔАОВ - равнобедренный ⇒
∠ОАВ=∠ОВА=(180°-45°):2=67,5°
ΔАВС , ∠АВС=90° , ∠САВ=67,5° ⇒ ∠АСВ=180°-90°-67,5°=22,5°
Или можно сразу сказать, что из того, что центральный угол ∠АОВ=45° опирается на дугу АВ . Вписанный угол ∠АСВ, опирающийся на ту же дугу АВ , равен половине центрального угла, то есть ∠АСВ=1/2*∠АОВ=1/2*45°=22,5° .