Найдем периметр 1ого участка
(60*2+100*2)м=320м
Найдём площадь первого участка:
S1=a*b
S1=6000м
Периметр перыого участка=периметру второго.
Периметр квадрата определяется по формуле:
P=4a
где Р-периметр квадрата, а  - сторона.
- сторона.
По этой формуле находим сторону квадрата
a=80м
Формула нахождения площади квадрата:
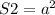
По ней находим площадь квадрата
S2=6400м
Площадь второго участка больше площа первого.
P.S. По одной из теорем: площадь квадрата больше площади прямоугольника, при одинаковых периметрах и при условии P>16
Угол между меньшей диагональю и большей боковой
стороной раваен 90°.
Объяснение:
Пусть дана прямоугольная трапеция АВСD с прямыми углами А и В. В прямоугольном треугольнике АВС катет АВ по Пифагору равен
АВ = √(АС²-ВС²) = √(15²-9²) = 12 ед. Опустим высоту СН.
СН = АВ = 12 (противоположные стороны прямоугольника).
Тогда в прямоугольном треугольнике HCD по Пифагору:
НD = √(CD²-CH²) = √(20²-12²) = 16 ед.
AD = AH+HD = 9+16 = 25 ед.
В треугольнике АСD стороны равны:
АС=15ед, CD = 20ед, (дано), a AD = 25 ед (найдено выше).
Следовательно, треугольник АСD - прямоугольный с прямым углом ACD, так как выполняется условие AD² = AC²+CD² (проще говоря, треугольник Пифагоров с соотношением сторон 3:4:5).
ответ: угол между меньшей диагональю и большей боковой
стороной равен 90°.