ответ: 27*. 54*. 99*.
Объяснение:
Решение.
Сумма всех углов треугольника равна 180*.
пусть один из углов равен 3х. Тогда второй равен 6х, а третий 11х градусов.
3х+6х+11х=180*.
20х=180*.
х=180*/20.
х=9*.
Один из углов равен 9*3=27*.
второй угол равен 9*6 = 54*.
третий угол равен 9*11=99*.
Проверим:
27*+54*+99*=180*. Всё верно!
![\sqrt[n]{x}](/tpl/images/0258/0436/b773b.png)
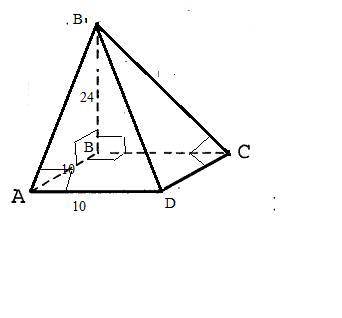
Основанием пирамиды является квадрат со стороной 10 см. Одно боковое ребро перпендикулярно плоскости основания и равно 24 см.
Вычисли площадь боковой поверхности.
Объяснение:
1)S(бок)=S(МВА)+S(МВС)+S(МАD)+S(МСD).
2)ΔМВА=ΔSМВС как прямоугольные по двум катетам⇒S(МВА)=S(МВС)=1/2*24*10=120 (см²).
Найдем МС= МА=√(24²+10²)=√676=26(см)
3)Т.к. прекция ВА⊥AD, то и наклонная МА⊥AD⇒ΔМAD-прямоугольный.
Т.к. прекция ВС⊥СD, то и наклонная МС⊥СD⇒ΔМСD-прямоугольный.
S(МАD)=S(МСD) как площади равных прямоугольных треугольников по катету и гипотенузе .
S(МАD)=S(МСD)=1/2*10*26=130 (см²)
4)S(бок)=2*120+2*130=500 (см²)
27°; 54°; 99°
Объяснение:
Сумма всех углов в треугольнике равна 180, следовательно:
3х+6х+11х =180
20х=180
х= 9
3×9= 27°
6×9= 54°
11×9= 99°