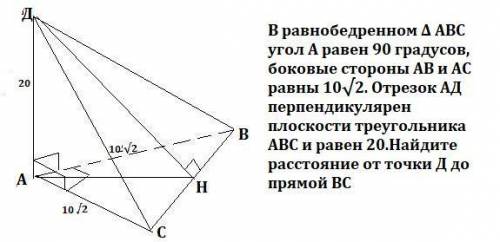
В равнобедренном Δ ABC угол А равен 90 градусов, боковые стороны AB и АC равны 10√2. Отрезок АД перпендикулярен плоскости треугольника АВС и равен 20.Найдите расстояние от точки Д до прямой ВС
Объяснение:
Пусть ДН⊥ВС. Тогда расстоянием от точки Д до прямой ВС будет отрезок ДН .
По т. о трех перпендикулярах АН⊥ВС.
1)ΔАВС-прямоугольный, по т Пифагора ВС=√((10√2)²+(10√2)² )=20.
2)В ΔАBС равнобедренном , высота АН является медианой ⇒
ВН=10 см.
3) ΔАВН -прямоугольный , по т. Пифагора ДH=√( (10√2)²-10²)= 10 (см).
х(5х-6)=0
х1=0 или 5х-6=0
5х=6
х2=1,2
ответ: 0
2) 5х^2 - 6х=0
ответ:1,2
3) 25х^2 - 1=0
25х^2=1
х^2=1/25
х=√1/25
х1=1/5
х2=-1/5
ответ:-1/5
4) 5х^2 - 6х +1=0
х1/2=6+-√36-4*5*1/10=6+-√16/10= 6+-4/10
х1=6+4/10=10/10=1
х2=6-4/10=2/10=0,2
ответ:1
5) 5х^2 - 6х +2=0
D=√36-4*5*2/10=√36-40/10=√-4/10
ответ:D<0
6) 5х^2 - 6х +2=0
ответ: нет корней
7) 25х^2 - 6х +0,36=0
D=√36-4*25*0,36/50=√36-36/50=0/50=0
ответ: D=0
8) 25х^2 - 6х +0,36=0
x1/2=6+-√36-4*25*0,36/50=6+- √36-36/50=6+-0/50=6/50
x1=6+0/50=6/50=0,12
x2=6-0/50=6/50=0,12
ответ:2 корня