1. По теореме Пифагора найдем гипотенузу.
Она равна √(9²+12²)=√(81+144)=15/см/
Пусть отрезки, на которые делит гипотенузу высота, проведенная к гипотенузе, будут х и (15-х)
Из равенства 9²=х*15, откуда х= 81/15=5,4, тогда другой отрезок равен 15-5,4= 9,6
Итак, один отрезок равен 5, 4см другой 9,6см.
Можно было бы решить и так. Квадрат другого катета, равного 12, есть произведение гипотенузы на проекцию этого катета на гипотенузу. Иными словами, 12²=у*15, где у- проекция катета на гипотенузу, откуда у =144/15=9,6.
Один отрезок равен 9,6см, тогда другой 15-9,6=5,4/см/
ответ 9,6см; 5,4см.
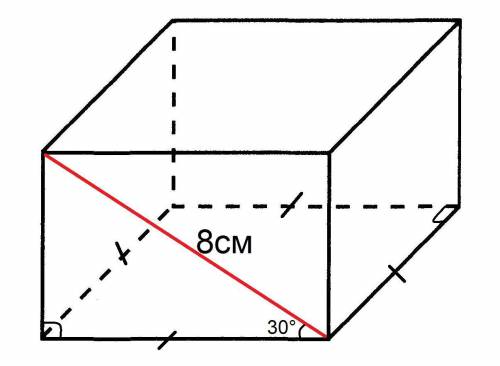
Рассмотрим один из двух треугольников, полученных при проведении диагонали в боковой грани параллелепипеда:
Треугольник прямоугольный т.к. параллелепипед прямой, по этой же причине один из острых углов равен 30°; гипотенуза (диагональ боковой грани) равна 8см; катет лежащий напротив угла в 30° (боковое ребро) равен половине гипотенузы: 8см:2 = 4см; другой катет (сторона основания), по теореме Пифагора, равен √(8²-4²) = √(64-16) = √48 см.
Объём параллелепипеда можно найти через его высоту (в нашем случаи это и боковое ребро) и площадь основания. В основании лежит квадрат, поэтому его площадь равна (√48 см)² = 48 см².
Тогда объём равен 4см · 48см² = 192 см³
ответ: 192см³.
согласен с табой человек