Найдём МС
МС² = ВС² + МВ² = 9 + 16 = 25
МС = 5
СД перпендикулярно плоскости треугольника ВСМ, следовательно, ВС перпендикулярно любой прямой в плоскости ВСМ. Таким образом Угол МСД тр-ка МСД = 90°.
Площадь прямоугольного тр-ка равна половине произведения катетов:
S = 0.5·MC·CД = 0,5·5·3 = 7,5
ответ. Площадь тр-ка МСД равна 7.5 см²

1)
или вот рисунок
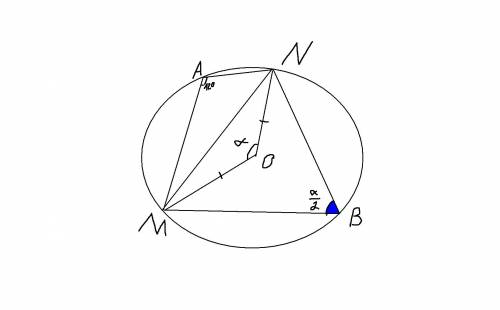
Около четырёхугольника можно описать окружность тогда и только тогда, когда сумма противоположных углов равна 180 , возьмем такую точку А на меньшей дуге, и на большой точку В , углы AMB+ANB=180 гр , угол В = 180-120=60
угол NBM вписанный и равен половине центрального то есть 120 гр, и через равнобедренный треугольник NOM
найдем по теореме косинусов MN
MN^2 =2*8^2-2*8^2*cos120
MN=√192 = 8√3
2)
площадь ромба
S=d1*d2/2
стало 1.1d1 , другая 0.85d2
S=1.1*0.85*d1*d2/2 = 0.935*d1*d2/2
то есть 1-0,935 = 0,065 уменшиться на 6,5 %
1) Чтобы определить дос таточно найти длину АВ, АС, ВС
(Формула: 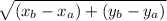
АВ=корень из ((1-0)^2+(-1-0)^2)=корень из (1+1)=корень из двух
ВС=корень из ((4-1)^2+(2-(-1))^2)=корень из (9+9)=корень из 18
АС=корень из ((4-0)^2+(2-0)^2))=корень из (16+4)=корень из 20
Если внимательно посмотреть, то мы увидим прямоугольный треугольник, с катетами АВ и ВС, гипотенузой АС. Можно это проверить теоремой Пифагора:
(корень из 2)^2+(корень из 18)^2=(корень из 20)^2
Все подходит, значит треугольник прямоугольный.
А под второй задачей неясно, что именно надо найти
Треугольник MCD - будет прямоугольный по теореме о трех перпендикулярах. Гипотенуза у него MD, катеты: DC=3, MC=5 (по т.Пифагора из тр-ка МВС)
Площадь тр-ка MCD = (1/2) * 3 * 5 = 7,5