126°
Объяснение:
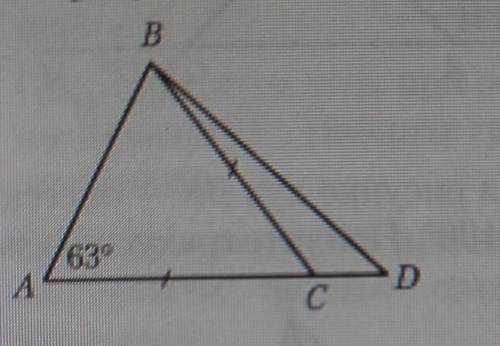
триуг. АВС — равнобедренный (АС=ВС)
Углы при основе (АВ) ровны:
угол САB=CBA=63°
Если сума градусных мер углов 180°, то угол ВСА=180°-63°-63°=54°
Если ВСА смежный с ВСD, то
ВСD=180°-54°=126°
.
вродь так
ромб - параллелограмм, у кот.все стороны равны
диагонали ромба перпендикулярны и делятся точкой пересечения пополам (как и у любого параллелограмма)
диагонали ромба - биссектрисы его углов
ромб ABCD AB=BC... AB=BD => треугольник ABD - равносторонний
в равностороннем треугольнике все стороны и все углы равны => BAD = 180/3=60 = BDA = DBA
BD - биссектриса CDA => CDA = 2BDA = 2*60 = 120
BAD = BCD, CDA = CBA (т.к. ромб - это параллелограмм)
вторая диагональ AC = AO + OC
из ABO (AB=10, BO=5) по т.Пифагора AO = корень(10*10-5*5) = корень(100-25) = корень(75) = корень(25*3) = 5*корень(3)
126°
Объяснение:
треугольник АВС равнобедренный так как АС=ВС. В равнобедренном треугольнике углы при основании равны, значит угол СВА равен углу САВ и равен 63°. Угол АСВ равен 54°, так как сумма углов треугольника равна 180° и 180°-(63°+63°)=54°. Угол DСВ равен 180°-54°=126° так как угол АСВ и угол DCB смежные