9.6
Объяснение:
Проведем две высоты в трапеции, как приведено на рисунке. Отрезок, заключенный между высотами, по теореме Фалеса будет одним и тем же, то есть равным 6 см, значит оставшаяся часть - это 20 см. Если за x обозначить одну из частей, тогда 20 - x будет второй фрагмент этих 20 см.
Рассматривая прямоугольные треугольники и взяв на вооружение тот факт, что высота в данной трапеции будет одинаковой, можно решить уравнение:
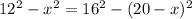
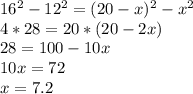
Подставив это значение в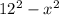 
, мы получим 92.16, а извлекая корень, получится 9.6
Дана равнобедренная трапеция АВСД. АВ и СД - боковые стороны. ВС - меньшее основание. По условию (и св-вам равнобедренной трапеции) АВ=СД=ВС
Проведем диагональ ВД. По условию угол АВД=120 градусов.
Проведем вторую диагоняль СА. (точка их пересечения О)Треугольник ВСО равнобедренный (по свойствам равн. трапеции), где ВО=ОС и угол ОВС=углу ВСО = х.
Треугольник АВС тоже равнобедренный. У него АВ=ВС (по условию) => Угол ВАС=углу ВСА(или ВСО) => угол АВС=углу ВСО=углу ОВС = х.
Найдем чему равен х:
120+х это угол АВС
120+х+х+х=180
3х=60
х=20 градусов.
Следовательн, углы при меньшем основании = 120+20=140 градусов (каждый по 140)
Углы при большем основании = (360-140-140):2=40 градусов (каждый по 40)
4
Пусть точка пересечения АВ с прямой из вершины С к прямой АВ будет точка К.
А точка, в которой высота к AC из вершины В пересекает АС будет D.
Рассмотрим треугольник АВD. Так как ВD – это высота в АВС, следовательно, она образует прямой угол с AС, то есть АВD – прямоугольный треугольник. Нам известна длина гипотенузы АВ = 8 и угол при катете АD - 15º.
Найдем AD:
AD = cos15º * 8 = √(2 + √3) / 2 * 8 = 7,73.
Теперь рассмотрим треугольник АКС. КС – это минимальное расстояние от С до АВ, значит КС перпендикулярно АВ.
Треугольник АКС также прямоугольный, с гипотенузой АС и углом против катета КС- 15º.
АС = AD * 2 = 7,73 * 2 = 15,46.
КС = sin15º * 15,46 = √(2 - √3) / 2 * 15,46 = 4.