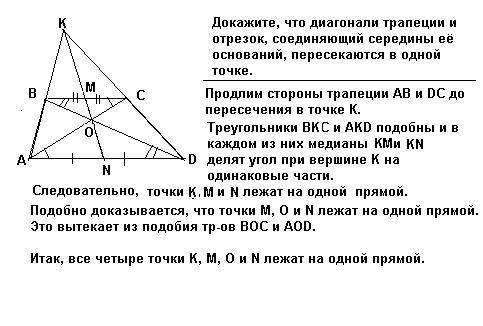
можно исходить из того, что треугольники при основаниях трапеции подобны. Части указанного отрезка медианы треугольников, которые выходят из точки пересечения диагоналей. Значит точка пересечения диагоналей принадлежит отрезку, соединяющему середины оснований трапеции
1 задача:
Доведения:
Рассмотрим ΔABD и ΔАВС
1) АВ = ВС (ΔАВС - равнобедренный с основанием АС)
2) AD = DC (ΔАВС - равнобедренный с основанием АС)
3) BD - общая.
Итак, ΔABD = ΔСВС за III признаком piвностi треугольников.
3 этого следует, что ∟ABD = ∟CBD. Тогда BD - биссектриса ∟АВС.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой, поэтому АЕ = ЕС.
2 задача
Рассмотрим ΔАВС - равнобедренный (АВ = ВС),
тогда ∟А = ∟C (свойство равнобедренного треугольника).
Рассмотрим ΔАВК и ΔСВМ.
1) АВ = ВС (по условию)
2) ∟А = ∟C (ΔАВС - равнобедренный)
3) ∟ABK = ∟CBM (по условию).
Итак, ΔАВК = ΔСВМ за II признаком piвностi треугольников.
3 этого следует pавность всех соответствующих Элементы, а именно ВМ = ВК.
ответ: ∠ВАС = ∠ВСА = 30 ° ; ∠АВС = 120° .
Условия задачи:
Δ АВС - равнобедренный , следовательно:
Боковые стороны равны ⇒ АВ=ВС = 14,2 см
Углы при основании равны :
АС - основание ⇒ ∠BAC (∠BAD) = ∠BCA (∠BCD)
BD =7,1 см - высота к основанию АС ⇒ является медианой и биссектрисой :
∠BDA = ∠BDC = 90° ( т.к. BD - высота)
AD = DC = АС/2 (т. к. BD - медиана)
∠ABD = ∠CBD (т. к. BD - биссектриса)
ΔBDA = ΔBDC - прямоугольные треугольники
Решение.
1) ΔBAD
По условию катет BD = 7,1 см , гипотенуза АВ = 14,2 см , следовательно :
BD = 1/2 * AB = 1/2 * 14,2 = 7,1 см
Если катет равен половине гипотенузы, то угол лежащий против этого катета равен 30° ⇒∠DAB (∠ BAC) = 30°
Проверим по определению синуса:
sin A = 7/14 = 1/2 ⇒ ∠BAC (∠BAD ) = ∠BCA (∠BCD) = 30°
2) ΔАВС :
Сумма углов любого треугольника = 180°
∠АВС = 180° - (∠ВАС + ∠ВСА)
∠АВС = 180 - 2*30 = 120 °
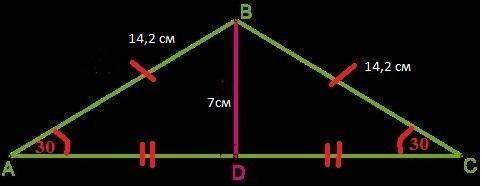
Решение прилагается во вложенном рисунке.