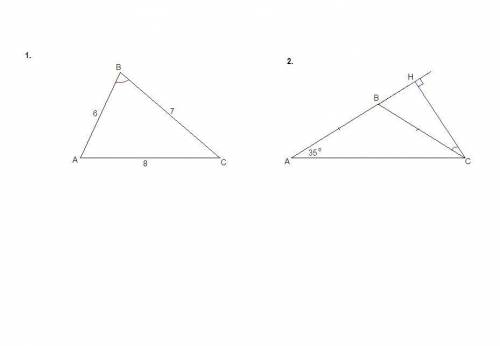
ответ:1.
По теореме косинусов:
АС² = АВ² + ВС² - 2·АВ·ВС·cos∠B
64 = 36 + 49 - 2·6·7·cos∠B
cos∠B = (36 + 49 - 64) / (2 · 6 · 7) = 21 / (2 · 6 · 7) = 1/4
Основное тригонометрическое тождество:
sin²∠B + cos²∠B = 1
sin∠B = √(1 - cos²∠B) = √(1 - 1/16) = √15/4
2.
СН - высота, проведенная к боковой стороне.
∠ВСН - искомый.
Углы при основании равнобедренного треугольника равны:
∠А = ∠С = 35°
∠НВС = ∠А + ∠С = 70°, так как внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
ΔНВС: ∠ВНС = 90°, ∠НВС = 70°, ⇒ ∠ВСН = 20°
Объяснение:
1)
Дано:
Δ ABC
∠А = 90°
АВ = 20 см
высота АD = 12 см
Найти:
АС и COS ∠С.
Найдем DB (по теореме Пифагора)
DВ² = АВ² - АD² = 400 - 144 = 256
DВ = 16 (см)
ΔАВС ~ ΔDВА по первому признаку подобия (два угла равны угол В-общий, ∠АDВ =∠ВАС =90°), =>
DВ/АВ = АВ/СВ
16/20 = 20/СВ
СВ = 20 · 20 :16 = 25
АС² = СВ² - АВ² =25² - 20² = 625 - 400 = 225
АС = 15 (cм)
Найдем сos C:
сos C = АС/СВ = 15/25 = 3/5
ответ: сos C = 3/5, АС = 15 см.
2)
рассмотрим треугольник ABD, угол D=90 угол A=60 по условию, следовательно, угол B=30, т.к. угол B=30 то AD=AB/2=6, а BD=AD*корень из 3=6*корень из трёх. S параллелограмма =BD*AD=6корней из 3*6=36 корней из 3
3)смотри фотографию

Обе задачи решаются однотипно.
Площадь сферы находят по формуле
S=4πR²
Для наглядности сделаем схематический рисунок осевого сечения шара, перпендикулярного данному сечению .
Сечение шара - круг. На рисунке он в разрезе выглядит линией.
АВ - его диаметр, а МВ- радиус.
ОМ - расстояние от центра круга до центра плоскости сечения, ОВ- радиус шара.
1) В шаре на расстоянии 12 см от центра проведено сечение
площадью 64 п
Найти площадь поверхности сферы.
Найдем квадрат радиуса сечения из его площади .
S=πr²
64π=πr²
r²=64
Из прямоугольного треугольника ОМВ по т.Пифагора найдем R² шара.
R²=64+144=208
S=4πR²=4*208π=832π
2)
Площадь сечения, удаленное от центра шара на 21 см, равна 784 п
Найти площадь поверхности сферы.
Найдем квадрат радиуса сечения из его площади .
784π=πr²
r²=784
R²=784+21²=441
S=4πR²=4π*441=1764π
------------------------
Если есть необходимость, можно вычислить площадь, умножив на π- в этом калькулятор.