ответ: S=π•[(ab/(a+b)]²
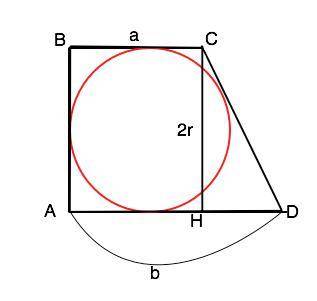
Объяснение: Обозначим трапецию АВСD, ВС||AD, СВА=ВАD=90°. ВС=а, AD=b.
Формула площади трапеции
Ѕ=0,5•(а+b)•h
Высота трапеции равна диаметру вписанной окружности=2r ⇒
S=(a+b)•2r/2 ⇒
r=S/(a+b)
Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований. S=ab
ab=(a+b)•r ⇒ r=ab/(a+b)
S(круга)=πr²
S=π•[(ab/(a+b)]²
* * *
Несложно доказать, что в такой трапеции S=ab, если соединить вершины С и D с центром окружности и выразить r=высоту прямоугольного ∆ СОD из произведения отрезков касательных, но это уже другая задача.
* * *
Задачу можно решить и другим
Если в четырехугольник вписана окружность. суммы длин его противоположных сторон равны.
Тогда АВ+CD=a+b. В прямоугольном треугольнике СНD по т.Пифагора СН²=СD²-DH²
CH=2r, HD=AD-BC=b-a, а CD=a+b-2r. Найденный радиус также будет ав/(а+в)
ответ: S=π•[(ab/(a+b)]²
Объяснение: Обозначим трапецию АВСD, ВС||AD, СВА=ВАD=90°. ВС=а, AD=b.
Формула площади трапеции
Ѕ=0,5•(а+b)•h
Высота трапеции равна диаметру вписанной окружности=2r ⇒
S=(a+b)•2r/2 ⇒
r=S/(a+b)
Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований. S=ab
ab=(a+b)•r ⇒ r=ab/(a+b)
S(круга)=πr²
S=π•[(ab/(a+b)]²
* * *
Несложно доказать, что в такой трапеции S=ab, если соединить вершины С и D с центром окружности и выразить r=высоту прямоугольного ∆ СОD из произведения отрезков касательных, но это уже другая задача.
* * *
Задачу можно решить и другим
Если в четырехугольник вписана окружность. суммы длин его противоположных сторон равны.
Тогда АВ+CD=a+b. В прямоугольном треугольнике СНD по т.Пифагора СН²=СD²-DH²
CH=2r, HD=AD-BC=b-a, а CD=a+b-2r. Найденный радиус также будет ав/(а+в)

Есть трапеция АВСД, где углы А и Д прямые. Вписана окружность с центром О. Точки К, Л, М - точки пересечения окружности со сторонами АВ, ВС и СД соответственно. ВЛ=4 и ЛС=25. Найти высоту.
ВК=ВЛ=4 и СЛ=СМ=25 по теореме о 2-х касательных, проведенных из одной точки.
Рассмотрим прямоугольную трапецию КВСМ. Из т.В проведем высоту ВН к стороне МС: КВ=МН.
НС=МС-МН=МС-КВ=25-4=21
ВН^2=BC^2-HC^2=(4+25)^2-21^2=841-441=400
BH=20