Найти точки пересечения окружности и прямой, заданных уравнениями
x^2 + y^2 = 1 и y = 3x + 1 . Вложение номер 1
Написать уравнения прямой, проходящей через точки (2 ; 4) и (-2 ; 4,5) .—не знаю
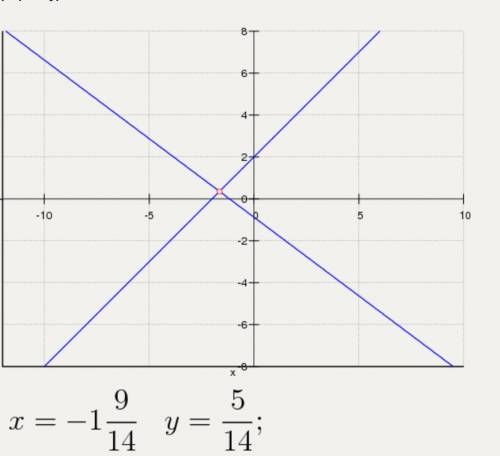
Найти точки пересечения прямых -x + y - 2 = 0 и 6x + 8y +7 = 0. Вложение номер 2
Написать уравнение окружности с центром в точке M(2 ; -1) и радиусом 3. —не знаю
Две стороны треугольника равны 17 см и 25 см. Высота делит третью сторону на отрезки, разность которых равна 12 см. Найти периметр треугольника.
Обозначим часть стороны, которая образована высотой и углом, за х. Тогда вторая часть - 12+х
Составим два уравнения по т Пифагора.
Х^2+h^2=17*17
(12+X)^2 +h^2=25*25
Теперь сделаем из этого одно уравнение
Х^2+25*25-(12+X)^2=17*17
X^2-144-24X-X^2=17^2-25^2
-144-24x=(17-25)(17+25)
144+24x=336
24x=192
x=8
тогда вся сторона у нас равна 2x+12=16+12=28 см
Периметр равен 17+25+28=70см

Vпризмы = Sоснования * H
обозначим сторону основания (квадрата) а
V = a^2 * H
Sбок = 4*a*H = 96
a*H = 96/4 = 24
V = a*a*H = a*24
осталось найти сторону основания...
по т.Пифагора (AC1)^2 = H^2 + AC^2
72 = H^2 + 2a^2
36 = 24*12/a^2 + a^2
36*a^2 - a^4 - 24*12 = 0
a^4 - 36*a^2 + 24*12 = 0
D = 36*36 - 4*24*12 = 4*36*(9-8) = (12)^2
(a^2) = (36 - 12)/2 = 24/2 = 12 или
(a^2) = (36 + 12)/2 = 48/2 = 24 отрицательные корни не рассматриваем =>
a = V12 = 2V3 или а = V24 = 2V6
V = 48*корень(3) или V = 48*корень(6)
интересно ---как-то впервые объем получился в двух вариантах...
ошибки не вижу... не понятно...