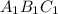 - его проекция на плоскость P.
- его проекция на плоскость P. 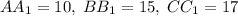 .
.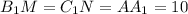 дм. Тогда BM = 15-10 = 5 дм, CM = 17-10 = 10 дм.
дм. Тогда BM = 15-10 = 5 дм, CM = 17-10 = 10 дм.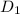 . Этот перпендикуляр разделит отрезок NM пополам. Значит
. Этот перпендикуляр разделит отрезок NM пополам. Значит 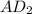 медиана треугольника
медиана треугольника 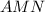 .
.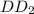 - средняя линия трапеции BCNM. Его длина
- средняя линия трапеции BCNM. Его длина 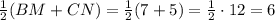 дм.
дм.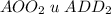 подобны по первому признаку:
подобны по первому признаку:  - общий,
- общий, 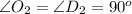 .
.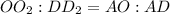
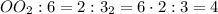 дм.
дм.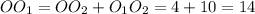 дм.
дм.
По условию задачи треугольники подобны, в подобных треугольниках углы равны.
Дано, что угол КАС - тупой, в треугольнике АВС тупым будет угол, который лежит против большей стороны - 2√3 - это угол ABC=углу КАС, а угол АКС=углу АСВ.
Косинус угла АСВ найдем по теореме косинусов: с²=а²+b²-2ab*cosα
cos ACB = cos AKC = [1²+(2√3)²-√7²]/2*1*2√3 = 6/(4√3)= (√3)/2