1.В прямоугольном треугольнике АВС(∟С= 90˚) проведена медиана СМ, длина которой 7 см, ∟А= 60˚. Найдите АС и АВ.
2.Угол между биссектрисой и высотой, проведенными из вершины наибольшего угла прямоугольного треугольника равен 14˚. Найдите острые углы данного треугольника
3.Высота прямоугольного треугольника, отпущенная на гипотенузу, образует с одним из катетов угол 55˚. Найдите острые углы данного треугольника.
Сделать рисунок. Решение с полным обоснованием.
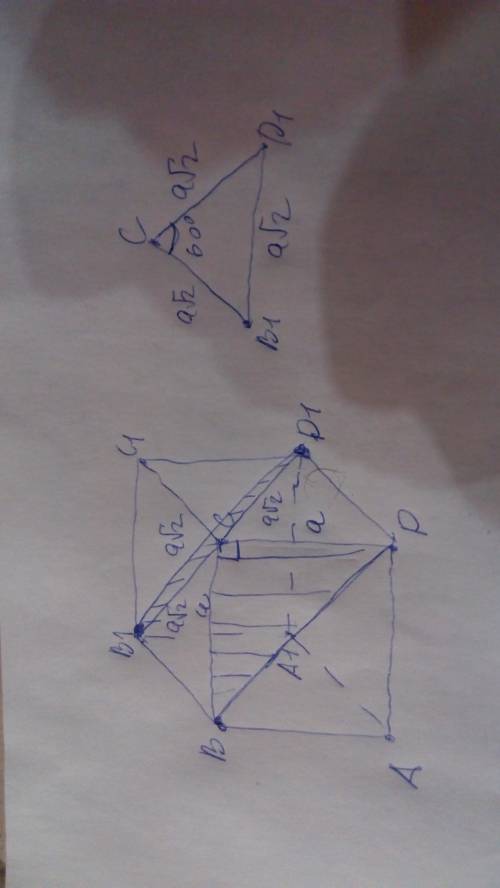
4 остальные стороны - следы сечения боковых граней призмы.
Они равны √(5²+(11/2)²) = √(25+30,25) = √55,25.
Высота шестиугольника равна √(АС²+СС1²) = √((2acos30°)²+11²) =
= √((2*5*(√3/2))² + 121) = √(75+121) = √196 = 14.
Площадь шестиугольника S равна сумме площадей прямоугольника S1 и двух треугольников, площадь S2 которых можно найти по формуле Герона.
S1 = 5*14 = 70.
S2 = 2√(p(p-a)(p-b)(p-c), где р - полупериметр, равный (а+в+с)/2 =
= (14+2*√55,25)/2 = 7+√55,25 ≈ 14,43303.
Тогда S2 = 2*17,5 = 35.
ответ: S = 70 + 35 = 105.