Дано:
∆MKN. ME - висота (ME ┴ KN). FN - висота (FN ┴ MK).
ME ∩ FN = 0. OM = ON; MF = KE.
Довести: ∆MNK - рівносторонній.
Доведения:
Розглянемо ∆MOF i ∆NOE.
За умовою NF - висота (NF ┴ MK); ∟NFM = 90° i MЕ - висота; ∟MEN = 90°.
1) ∟MFO = ∟NEO = 90°;
2) ∟MOF = ∟NOE (вертикальні);
3) ОМ = ON.
За ознакою piвностi прямокутних трикутників маємо: ∆MFO = ∆NEO.
Звідси MF = EN.
За умовою MF = KE i MF = EN, тобто KE = EN.
За умовою ME - висота. Тоді AMKN - рівнобедрений, MK = MN.
Розглянемо ∆MFN i ∆NEM:
1) ∟MFN = ∟MЕN = 90°;
2) MF = EN;
3) MN - спільна сторона.
Тому ∆MFN = ∆NEM. Звідси ∟FMN = ∟MNE.
Отже, ∆MKN - рівнобедрений. MK = KN. Якщо MK = MN i MK = KN.
Тому ∆ABC - рівносторонній.
Доведено.
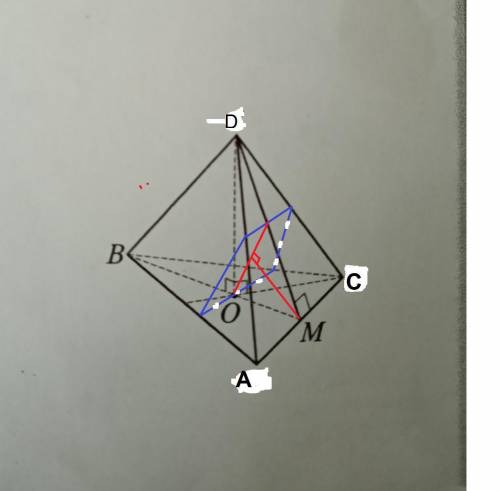
Дан правильный тетраэдр с ребром 3√6.
Так как сечение проходит через середины боковых рёбер, то линии сечения в плоскостях граней ABC и ADC параллельны ребру АС.
Поэтому расстояние от точки А до заданной плоскости равно этому же расстоянию от любой точки на прямой АС.
Проведём перпендикулярное сечение к заданной плоскости через апофему DM.
Получим равнобедренный треугольник ОТМ.
Боковые стороны его равны половине апофемы А.
А = 3√6*cos 30° = 3√6*(√3/2) = 9√2/2.
OT = TM = 9√2/4.
OM = A/3 = 9√2/6 = 3√2/2.
Решаем этот треугольник и находим высоту МЕ = 2, которая и есть расстояние до заданной плоскости.
Можно использовать формулу h = 2S/OT.
Высота пирамиды - правильного тетраэдра - равна а√(2/3) = 6.
Значит высота треугольника ОТМ = 6/2 = 3.
S = (1/2)*3*OM = (3/2)*3√2/2 = 9√2/4.
h = 2*(9√2/4)/(9√2/4) = 2.

Объяснение:
если ставь лайййк))