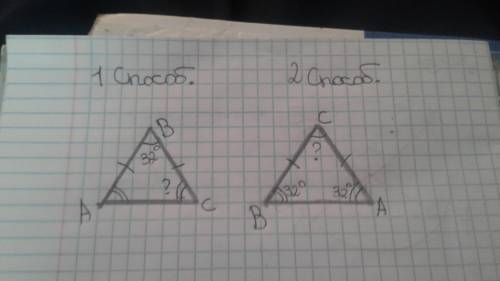
Так как АВ=ВС, то треугольник соответственно будет равнобедренным. Мы рассмотрим
Угол В при вершине будет равен 32 градусам. Чтобы найти угол ВСА нам надо, 180-32=148*. Мы нашли общую сумму двух углов при основании, а как мы знаем углы при основании у равнобедренного треугольника равны. Чтобы найти угол ВСА нам надо 148*:2=74*.
ответ:74*.
Теперь тут нам надо найти угол С при вершине. Нам известен угол В 32*, получается угол А тоже 32*. Потому что углы при основании равны. Чтобы найти угол ВСА нам надо из 180*-(32*+32*)=116*.
ответ: 116*
Объяснение:
Удачи!!;)
На шахматном турнире каждый из участников должен был сыграть ровно одну партию с каждым из прочих, но два участника выбыли из турнира, сыграв только по 3 партии. Поэтому число партий, сыгранных в турнире, оказалось равным 110. Сколько всего было участников турнира?
Объяснение:
Пусть первоначально участников было х.
Два участника, которые выбыли , сыграли по 3 партии т.е. :
1 случай ) 3+3=6 , если не играли межлу собой ;
2 случай) 3+2=5 , если одна партия была между выбывшими.
Значит партии, оставшиеся на остальных участников :
1 случай ) 110-6=104 (шт) ;
2 случай ) 110-5=105 (шт).
Оставшиеся участники (х-2) сыграли по одной партии. Таких пар это сочетание из (х-2) по 2 :
С(х-2;2)=104 , С(х-2;2)=104 ,
(х-2)!/(2! * (х -4)!) = 104 ; (х-2)!/(2! * (х -4)!) =105
(х-3) *(х -2)/2 =104 ; (х-3) *(х -2)/2 =105
х²-5х+6=104*2 ; х²-5х+6=105*2
х²-5х-202=0 ; х²-5х-204=0
D=833>0 , D=841>0, х₁=17,
Натуральных корней х₂=-15-не подходит по смыслу задачи.
нет .
Всего участников 17.
12√3 см²
Объяснение:
Дано: АВСД - трапеция, АВ=СД=4 см, ВС=4 см, ∠АВС=120°. Найти S(АВСД).
ΔАВС - равнобедренный, т.к. АВ=ВС, значит, ∠ВАС=∠ВСА=(180-120):2=30°
∠САД=∠ВСА=30° как внутренние накрест лежащие при ВС║АД и секущей АС
∠ВАД=∠Д=30+30=60°
Проведем высоты ВК и СН. Рассмотрим ΔСДН - прямоугольный.
∠Д=60°, ∠НСД=90-60=30°, значит ДН=1/2 СД=2 см по свойству катета, лежащего против угла 30°; АК=ДН=2 см;
АД=АК+КН+ДН=2+4+2=8 см
Найдем высоту трапеции по теореме Пифагора
СН=√(СД²-ДН²)=√(16-4)=√12=2√3 см.
S=(ВС+АД):2*СН=(4+8):2*2√3=12√3 см²