ТЕКСТ ЗАДАНИЯ В параллелограмме, площадь которого 72 см?, стороны равны 6 см и 10 см. Найди его высоты. / Прикрепи тут фотографию полного канонического решения
Как известно количество вершин и сторон в любом многоугольнике совпадает, пускай в нашем случае их будет х,
дальше будем рассуждать следующим образом: чтобы узнать число диагоналей каждую вершину соединяем с другими вершинами, кроме нее самой и соседних, получаем х *(х-3), но так как при таком соединении диагонали повторяются 2 раза, то их число в х-угольнике будет х*(х-3)/2
по условию имеем соотношение (х*(х-3)/2)/х = 2,5 х² - 3х = 5х х² - 8х = 0 х = 0 либо х = 8 первый корень не удовлетворяет условию,значит х = 8 ответ: 8
Как известно количество вершин и сторон в любом многоугольнике совпадает, пускай в нашем случае их будет х,
дальше будем рассуждать следующим образом: чтобы узнать число диагоналей каждую вершину соединяем с другими вершинами, кроме нее самой и соседних, получаем х *(х-3), но так как при таком соединении диагонали повторяются 2 раза, то их число в х-угольнике будет х*(х-3)/2
по условию имеем соотношение (х*(х-3)/2)/х = 2,5 х² - 3х = 5х х² - 8х = 0 х = 0 либо х = 8 первый корень не удовлетворяет условию,значит х = 8 ответ: 8
Высоты равны: 12 и 7,2
Объяснение:
Площадь параллелограмма равно произведению основания (стороны на высоту): S=a*h.
S=72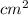
Тогда h1=S/a=72/6=12 см, а h2=S/b=72/10=7,2 см.