Question

Найти значение параметра а,при которых плоскости п1 и п2 параллельны(перпендикулярны). п1: 7х-ау+5az=0 п2: -x-y+5z=2

Answer 1

Чтобы плоскости были параллельны, надо, чтобы их нормальные векторы были параллельны.

Нормальный вектор П1 будет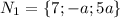 $N_1=\{7;-a;5a\}$

Нормальный вектор П2 будет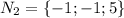$N_2=\{-1;-1;5\}$

Чтобы вектора были параллельны, надо, чтобы они различались всего лишь на какую-то константу, отличную от нуля. То есть кординаты первого вектора выражались через координаты второго вектора, умноженного на константу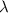 $\lambda$.

Получаем систему уравнений

$\begin{cases} -1*\lambda=7\\-1*\lambda=-a\\5*\lambda=5a \end{cases}$

Из первого уравнения получаем, что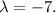 $\lambda=-7.$

Второе и третье уравнения упростим и получим следующую систему

$\begin{cases} \lambda=a\\\lambda=a \end{cases}$

То есть а=-7. В этом случае плоскости параллельны.

Чтобы плоскости были перпендикулярны, надо чтобы скалярное произведение нормальных векторов равнялось нулю.

Надо перемножить все координаты между собой и приравнять их нулю

$7*(-1)+(-a)*(-1)+5a*5=0$

$-7+a+25a=0$

$-7+26a=0$

$26a=7$

$a=\frac{7}{26}$

при а=-7 - плоскости параллельны,

при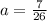 $a=\frac{7}{26}$ - плоскости перпендикулярны.