
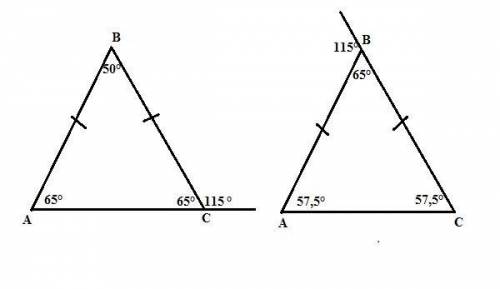
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.
Объяснение:
Объем пирамиды вычисляется по формуле 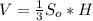 , где
, где 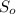 - площадь основы. Пирамида правильная, значит AB = BC = CD = DA = a - сторона основы, а основа - квадрат, значит
- площадь основы. Пирамида правильная, значит AB = BC = CD = DA = a - сторона основы, а основа - квадрат, значит 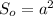 .
.
===================
Сперва можем найти высоту.
Из прямоугольного ΔASO по соотношениям найдем катет. Знаем гипотенузу и противолежащий катет, а значит:
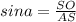 =>
=> 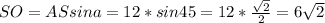 .
.
===================
Теперь нужно найти площадь основы 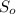 , сделать это можно с диагоналей. Диагональ можно найти опять же из треугольника ASO.
, сделать это можно с диагоналей. Диагональ можно найти опять же из треугольника ASO.
Соотношение прилежащего катета и гипотенузы: 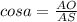 =>
=> 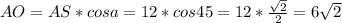 - только половина диагонали квадрата; вся диагональ:
- только половина диагонали квадрата; вся диагональ: 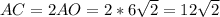 .
.
Есть формула диагонали квадрата: 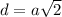 , из неё выразим сторону =>
, из неё выразим сторону => 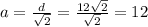 - сторона основы.
- сторона основы.
Найдем площадь основы 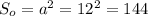 ед.²
ед.²
===================
Теперь можем найти объем пирамиды:
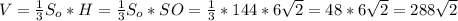 ед.³
ед.³
Внизу.
Объяснение:
Диагональ параллелепипеда можно найти по формуле: √a²+b²+c², где
a,b,c - наши измерения. Если подставить значения, то выдет √50=5√2 см
далее, если посмотреть на основание, то это прямоугольник со сторонами 3 и 4 см. по теореме Пифагора найдем диагональ или гипотенузу треугольника ABD: она равна 5 см.
из треугольника CBD: мы знаем CD=5√2; BD=5; BC= 5 по условию
BD=BC, значит треугольник CBD - равнобедренный, один из углов 90
значит оставшиеся два равны по 45 градусов.
ответ: 45 градусов; 5√2 см