ответ: r = 5*(4+√5)/11
Объяснение:
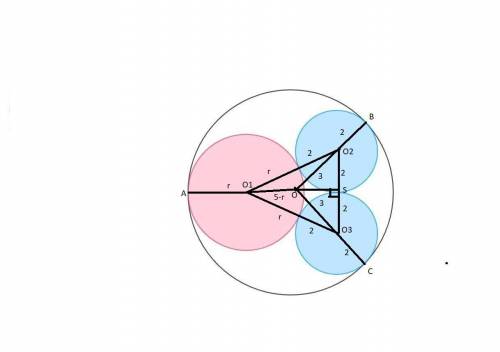
A,B,С - точки касания внутренних окружностей с внешней
O1,O2,O3 - центры внутренних окружностей
O-центр внешней окружности. (смотрите рисунок)
O1S- высота
r- радиус красной окружности
Из условий касания окружностей и симметрии имеем :
O1O=5-r
O1O2 =O1O3 = 2+r
O2S=O3S=2
OO2=OO3= 5-2 = 3
По теореме Пифагора:
OS = √(3^2- 2^2) = √5
O1S = 5+√5 -r
По теореме Пифагора:
(5+√5 -r)^2 = (2+r)^2 - 2^2
(2+r)^2 - (5+√5 -r)^2 = 4
(7+√5)*( -3-√5+2r) =4
-3-√5+2r = 4/(7+√5) = 4*(7-√5)/44 = (7-√5)/11
-33 - 11√5 +22r = 7-√5
22r = 40 +10√5
r = (20+5√5)/11 = 5*(4+√5)/11
Построение:
На прямой "а" возьмем произвольную точку А и из нее как из центра проведем окружность произвольного радиуса. Обозначим точку пересечения этой окружности с прямой "а" через "b" и "с" и из них, как из центров проведем окружности радиуса R=bс. Соединив точку пересечения "d" и "е" этих окружностей получим прямую, проходящую через точку А перпендикулярно прямой "а".
Доказательство:
Хорда de является общей хордой пересекающихся окружностей, следовательно, она перпендикулярна прямой, соединяющей центры этих окружностей (свойство). Эта хорда проходит через точку А на прямой "а", поскольку она равноудалена от точек "b" и "с", а точка А делит отрезок bс пополам по построению.