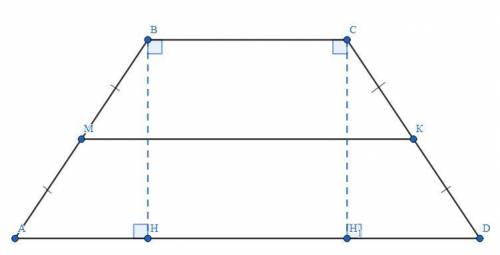
Четырёхугольник ABCD - равнобедренная трапеция (ВС║AD, AD > ВС, АВ = CD).
Отрезок ВН - высота, опущенная на основание AD (ВН⊥AD, ВН⊥ВС).
Отрезок МК - средняя линия.
AH : HD = 1 : 5.
HD = 35 см.
Найти :МК = ?
Решение :На основание AD из вершины тупого ∠С опустим высоту СН₁ (СН₁⊥AD, СН₁⊥ВС).
По свойству отрезков в равнобедренной трапеции, образованных основанием высоты на большем основании :
АН = DH₁.
Пусть АН = х, тогда, по условию задачи, HD = 5х.
HD = 5х
35 см = 5х
х = 35 см/5
х = 7 см.
АН = DH₁ = х = 7 см
AD = AH + HD = 7 см + 35 см = 42 см.
Рассмотрим четырёхугольник BHH₁C.
Все его углы прямые, значит, этот четырёхугольник - прямоугольник (признак прямоугольника).
AD = AH + HH₁ + DH₁
HH₁ = AD - AH - DH₁ = 42 см - 7 см - 7 см = 28 см.
Тогда ВС = НН₁ = 28 см (так как противоположные стороны прямоугольника равны).
Средняя линия трапеции равна полусумме её оснований.Следовательно :
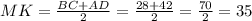 cм.
cм.
35 см.
4. Дан ромб ABCD.Выразите векторы BD и СA через AB и СD .
4. Дан ромб ABCD.Выразите векторы BD и СA через AB и СD
Задача с недостающими данными.
СD ничего не прибавляет к условию ( СD = - AB )
Поэтому , допустим СD задан вектор BC
BD = BA +AD = - AB + BC ; CA = CB + BA = - BC - AB = - ( AB +BC ) .
или коротко CA = - AC = - (AB +BC ) .
- - - - - - - - - - - - - - -
5. Дано: a(1 ; - 4) и b(3 ; -1) . Найдите 3a - 2b .
a = i - 4j ; b =3i -j ; 3a - 2b =3( i - 4j ) -2(3i -j) =3i -12j -6i+2j = -3i -10j .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
3a (3*1 ; 3(-4) ) ⇔ 3a (3 ; -12 ) ; -2b (-2*3 ; -2*(-1) ) ⇔ - 2b (- 6 ;2 )
3a - 2b = 3a +(- 2b) ( 3 - 6 ; - 12+2 ) 3a - 2b ( - 3 ; - 10 )
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
2b(2*3 ; 2*(-1) ) ⇔2b(6 ; -2 ) ; - 2b( -6 ; 2 )
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Объяснение:
У шара главный параметр - его радиус.
Найти его можно из условия:
30 = пи*r^2
r = V(30/пи) =V(30/3,14159) = 3,090194 см
R = V(12^2+r^2) =V(144+9,5493) = 12,3915 см