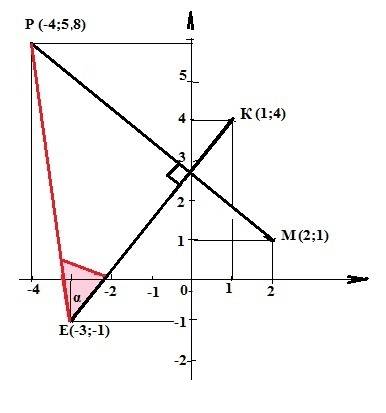
а) Условие перпендикулярности векторов: векторы "а" и "b" являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю, то есть когда Хa*Хb + Ya*Yb = 0, где X и Y - соответствующие координаты векторов. Координаты векторов равны разности соответствующих координат точек его конца и начала. Тогда вектор ЕК{1-(-3);4-(-1)} или ЕК{4;5}. Вектор РМ{2-(-4);1-(-a)} или РМ{6;1+a}. Тогда условие перпендикулярности векторов ЕК и РМ: 6*4+(1+а)*5 = 0. 24+5+5а=0. => а = - 5,8.
б) Угол между векторами определяется по формуле: cosα=(x1*x2+y1*y2)/[√(x1²+y1²)*√(x2²+y2²)]. ЕР{-4-(-3);5,8-(-1)) или ЕР{-1;6,8} (координату точки Yр= 5,8(-а) нашли в п.а). Координаты вектора ЕК{1-(-3);4-(-1)} или КЕ{4;5}. Тогда косинус угла между этими векторами будет равен:
cosα=(-4+34)/[√(1+46,24)*√(16+25)] = 30/44 ≈ 0,682. Угол между векторами по таблице равен 47°.
ответ: угол между векторами РЕ и КЕ равен ~47°.
ответ: А=С=70г.
В=D=110г.(100г.)
Объяснение: Дано: ABCD - ромб, угол ABO на 20г.(30г.) больше угла BAO.
Найти: углы- А, В, C, D.
Решение: Пусть угол ВАО равен x, по условию угол АВО на 20г.(30г.) больше угла ВАО следовательно угол АВО =x+20. Треугольник АВО - прямоугольный, так как по свойству ромба его диагонали взаимно перпендикулярны, следовательно сумма углов треугольника АВО = 180г. угол АОВ = 90г. Составим уравнение: x+x+20=90
2x=70
x=35
(x+x+30=90; 2x=60; x=30).
угол АВО равен x+20 следовательно угол АВО = 55г. (50г.)
Диагонали ромба являются его биссектрисами (по свойству диагоналей ромба) следовательно угол А = 2ВАО = 70г. угол В = 2АВО =110г.(100г.). По свойству ромба его противоположные углы равны, следовательно угол А = угол С = 70г.
угол В = угол D = 110г.(100г.)