Объяснение: квадрат диагонали параллелепипеда равен сумме квадратов его измерений:
Д²=дл²+шир²+выс²=
Д²=7²+6²+10²=49+36+100=185;
Д=√185см
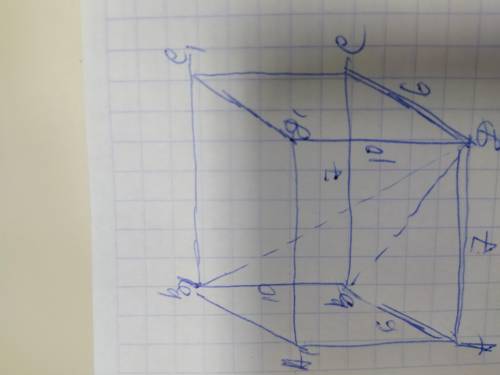
Если нужно найти диагонали граней параллелепипеда, тогда обозначим его вершины А В С Д В1 С1 Д1. Диагональ ВД делит грань АВСД на 2 равных прямоугольных треугольника, в которых стороны основания являются катетами а диагональ гипотенузой. Найдём диагональ ВД грани АВСД по теореме Пифагора: ВД²=АВ²+АД²=6²+7²=36+49=
=85; ВД=√85см. Такая же величина диагонали у грани А1В1С1Д1. Теперь найдём диагональ грани АА1ВВ1 также по теореме Пифагора:
АВ1²=АВ²+АА1²=6²+10²=36+100=136;
АВ1=√136=2√34см. Такая же величина диагонали у грани Д1ДС1С. Диагонали одной грани равны между собой.
Диагональ грани АА1ДД1=АД²+ДД1²=
=7²+10²=49+100=149; ДД1=√149см
Диагональ ДД1=√149см
піраміда КАВСД, К-вершина, АВСД-квадрат, О-центр основи-перетин діагоналей, КА=КВ=КС=КД=8, кут КАС=60=кут КСА, тоді кут АКС в трикутнику АКС=180-60-60=60, трикутник АКС рівносторонній, КА=КС=АС=8, АД=корінь(АС в квадраті/2)=корінь(64/2)=4*корінь2
проводимо апофему КН на АД, КН-висота=медіані, АН=НД=1/2АД=4*корінь2/2=2*корінь2, трикутник АКН прямокутний, КН=корінь(КА в квадраті-АН в квадраті)=корінь(64-8)=2*корінь14
бічна поверхня=1/2*периметрАВСД*КН=1/2*4*4*корінь2*2*корінь14=16*корінь28=32*корінь7