Грани пирамиды наклонены к плоскостью основания под равными углами, следовательно, проекции их высот на основание равны радиусу вписанной в треугольник (основание) окружности. ⇒
высоты боковых граней, как наклонные из одной точки с равными проекциями, равны.
Площадь S полной поверхности пирамиды - сумма площадей основания (S1) и боковой поверхности (S2).
S=S1+S2
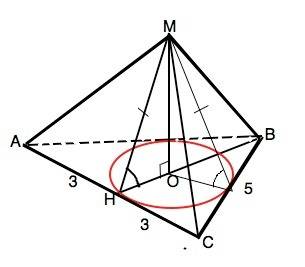
В основании пирамиды МАВС - равнобедренный треугольник АВС; АВ=ВС=5 см, АС=6 см.
Высота основания ВН делит треугольник на два равных прямоугольных треугольника.
ВН=√(AB²-AH²)=√(25-9)=4
ОН- радиус вписанной окружности. r=S/p, где р - полупериметр ∆АВС.
S1=BH•AC:2=12 см²
р=(5+5+6):2=8 см
r=12/8=1,5 см
МН=ОН:cos60°=1,5:1/2=3
S2=3•h=3*8=24 см²
S=12+24=36 см²
AD = (12+8√3)/3 см.
Объяснение:
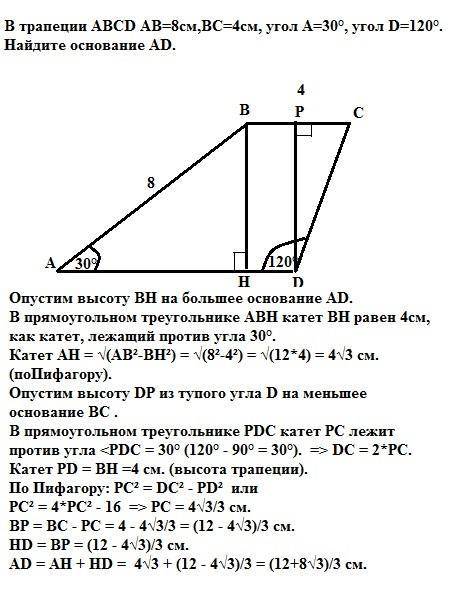
Опустим высоту ВН на большее основание AD.
В прямоугольном треугольнике АВН катет ВН равен 4см, как катет, лежащий против угла 30°.
Катет АН = √(АВ²-ВН²) = √(8²-4²) = √(12*4) = 4√3 см. (по Пифагору).
Опустим высоту DP из тупого угла D на меньшее основание ВС .
В прямоугольном треугольнике PDC катет PС лежит против угла
PDC = 30° (120° - 90° = 30°). => DC = 2*PC. Катет
PD = ВН =4 см. (высота трапеции).
По Пифагору: РС² = DC² - PD² или
РС² = 4*РС² - 16 => РС = 4√3/3 см.
ВР = ВС - РС = 4 - 4√3/3 = (12 - 4√3)/3 см.
HD = BP = (12 - 4√3)/3 см.
AD = AH + HD = 4√3 + (12 - 4√3)/3 = (12+8√3)/3 см.
30/√π
Объяснение:
Согласно нашему рисунку, площадь основания цилиндра есть не что иное как S=πr², a высота есть не что иное как h. Поскольку осевое сечение цилиндра является прямоугольником, его площадь равна 2rh. Заметим, что r=√(S/π). Значит, искомая площадь равна 2h√(S/π)=2*5*√(9/π)=30/√π. Значение этого выражения примерно равно 16,93