Раз график данной функции параллелен графику функци у = 3х - 1 >
что k = 3. Получаем у = 3х + b. Теперь в это ур-е подставим
координаты точки М(2; 1)
1 = 3*2 + b ---> b = -5
Получили функцию у = 3х - 5
Пересечение с осью ох х = 0 ---> y = -5
Пересечение с осью оу у = 0 ---> 3х - 5 = 0 ---> x = 5/3
Построй систему координат по оси оу отметь точку у = -5,
а по оси ох точку х = 1 целая 2/3 затем эти 2 точки
соедини прямой.
Пусть S₁ - это площадь бо́льшего треугольника, а S₂ - площадь меньшего треугольника.
Пусть k > 1 (это значит, что в числителе будет стоять бо́льший треугольник).
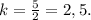
Отсюда -
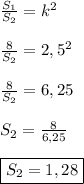
1,28 (ед²).
- - -
Случай 2 - Площадь меньшего треугольника равна 8 (ед²).В этом случае наоборот k < 1 (в числителе будет стоять меньший треугольник).
S₁ - площадь бо́льшего треугольника, S₂ - площадь меньшего треугольника
Тогда -
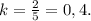
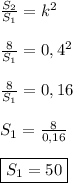
50 (ед²).
Теорема. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Доказательство. Пусть ABC – данный треугольник, O – центр вписанной в него окружности, D, E и F – точки касания окружности со сторонами. Прямоугольные треугольники AOD и AOE равны по гипотенузе и катету. У них гипотенуза AO общая, а катеты OD и OE равны как радиусы. Из равенства треугольников следует равенство углов OAD и OAE. А это значит, что точка O лежит на биссектрисе треугольника, проведённой из вершины A. Точно так же доказывается, что точка O лежит на двух других биссектрисах треугольника. Теорема доказана.
Объяснение:
Так как прямые параллельны, то угловые коэффициенты равны, k=3
Так как прямая проходит через точку М(2;1), то подставляем ее координаты в формулу:
1=3*2+b
1=6+b
b=-5
Если х=0, то: у=3*0-5=-5
Если у=0, то: 0=3х-5
3х=5
х=5/3
ответ: (0; -5) и (5/3; 0)